Lesson Example Discussion Quiz: Class Homework |
Quiz Discussion |
Title: Congruency of triangles (ASA) |
Grade: 10-a Lesson: S2-L2 |
Explanation: |
Quiz: Discussion in Class
| Problem Id | Question |
|---|---|
Steps 1 |
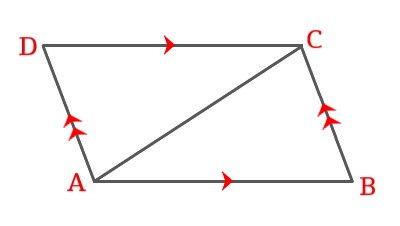
\$AB ∥ DC\$, \$AD ∥ BC\$ and \$AC\$ is the diagonal of the parallelogram \$ABCD\$. Prove \$\triangleABC \cong \triangleCDA\$.
|
Steps 2 |
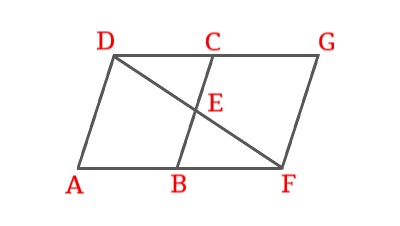
\$AB ∥ DC\$, E is the mid-point of BC, prove \$\triangleEBF \cong \triangleECD\$.
|
Steps 3 |
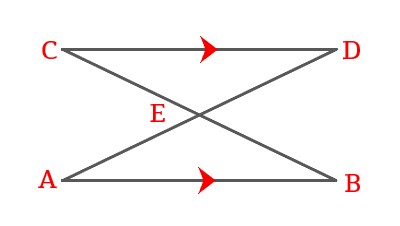
\$AB ∥ DC\$, E is the mid-point of BC, then show that \$\triangle AEB \cong \triangle DEC\$.
|
Steps 4 |
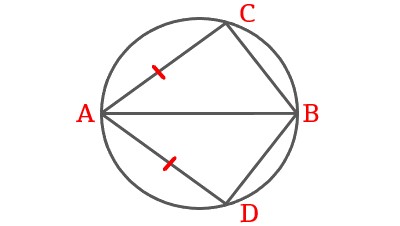
ACBD is a cyclic quadrilateral, AC = AD and AB bisects \$\angleA\$. Show that \$\triangle ABC \cong \triangle ABD\$.
|
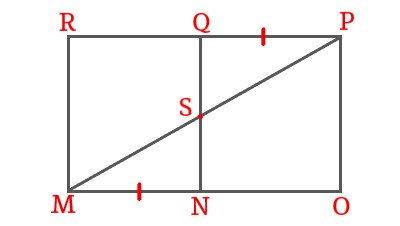
Steps 5 |
QN bisects RP and MO, S is the mid-point of QN and QP = MN, then show that \$\triangleMSN \cong \trianglePSQ\$.
|
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 26-November-2022 07:30 PM EST