Lesson Example Discussion Quiz: Class Homework |
Quiz At Home |
Title: Congruency of triangles (ASA) |
Grade: 10-a Lesson: S2-L2 |
Explanation: |
Quiz: at Home
| Problem Id | Question |
|---|---|
1 |
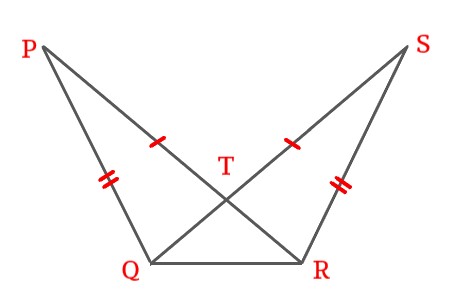
QR is the common side for \$\triangle PQR\$ and \$\triangle SRQ\$, then prove \$\triangle PQR \cong \triangle SRQ\$.
|
2 |
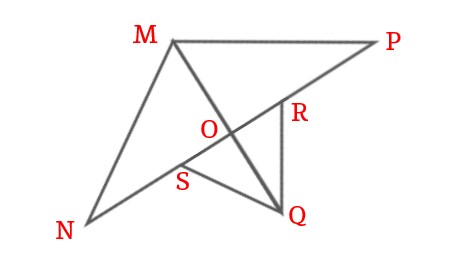
MQ is the angle bisector of \$\angle NMP\$ and O is the mid-point of NP, then prove \$\triangle MON \cong \triangle MOP\$.
|
3 |
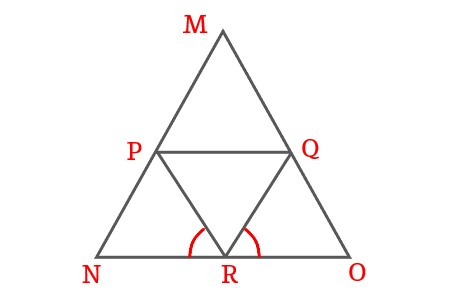
MNO is a equilateral triangle, P, Q and R are the mid-points of MN, NO and OM respectively and \$PQ ∥ NO \$. Prove \$\triangle MPQ \cong \triangle PNR\$.
|
4 |
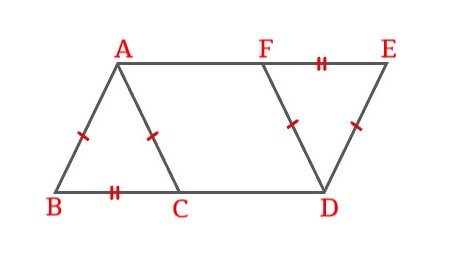
\$\triangle ABC\$ and \$\triangle DEF\$ are isosceles triangles and have equal aeras. Prove \$\triangle ABC \cong \triangle DEF\$.
|
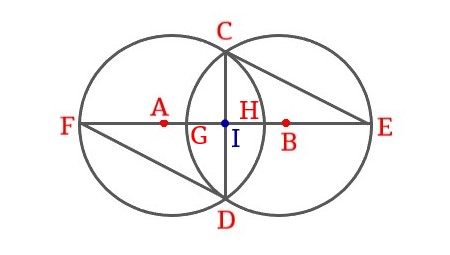
5 |
The two circles with centers A and B are orthogonal, CD is the common chord for the two circles, \$FE \bot CD\$ and I is the mid point of CD and FE. Prove \$\triangle CIE \cong \triangle DIF\$.
|
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 26-November-2022 07:30 PM EST