SaiBook.us Geometry

Home Course Section

Register Enroll Refer

Lesson Example Discussion Quiz: Class Homework

Step-2

Title:

Grade: 10-a Lesson: S2-L2

Explanation:

Description: 2

From the figure we can observe that

$d2$

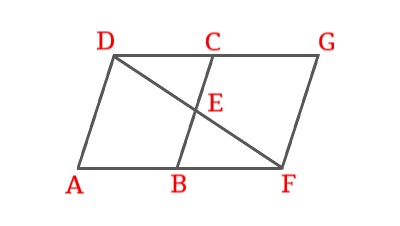
\begin{align} AB ∥ DC \tag{Given}\\ EB = EC \tag{Given}\\ \end{align}

Consider \$\triangle EBF\$ and \$\triangle ECD\$.

\begin{align} BE &= CE \\ \angle BEF &= \angle CED \tag{Alternate interior angles} \\ \angle EBF &= \angle ECD \tag{Alternate interior angles} \\ \end{align}

So, \begin{align} \triangle EBF \cong \triangle ECD \\ \end{align}

Henced proved that \$\triangleEBF\$ and \$\cong\$ \$\triangleECD\$ by the ASA congruence rule.

From the figure we can observe that
$d2$

Steps	Statment	Solution
1	Given	From the figure we can observe that
2	Given side of triangles	AB ∥ DC and EB = EC
3	Consider angles	\$\triangleEBF \cong \triangle ECD\$
4	side	BE = CE
5	Alternate interior angles	\$angle BEF = angle CED\$ and \$angle EBF = angle ECD\$
6	Congruency	\$\triangle EBF \cong \triangle ECD\$
7	Prove that	Henced proved that \$\triangleEBF\$ and \$\cong\$ \$\triangleECD\$ by the ASA congruence rule.

Steps

Statment

Solution

Given

From the figure we can observe that

Given side of triangles

AB ∥ DC and EB = EC

Consider angles

\$\triangleEBF \cong \triangle ECD\$

side

BE = CE

Alternate interior angles

\$angle BEF = angle CED\$ and \$angle EBF = angle ECD\$

Congruency

\$\triangle EBF \cong \triangle ECD\$

Prove that

Henced proved that \$\triangleEBF\$ and \$\cong\$ \$\triangleECD\$ by the ASA congruence rule.