Lesson Example Discussion Quiz: Class Homework |
Quiz Discussion |
Title: Congruency of triangles (SAS) |
Grade: 10-a Lesson: S2-L1 |
Explanation: |
Quiz: Discussion in Class
| Problem Id | Question |
|---|---|
Steps 1 |
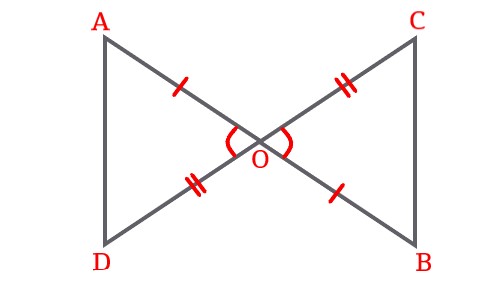
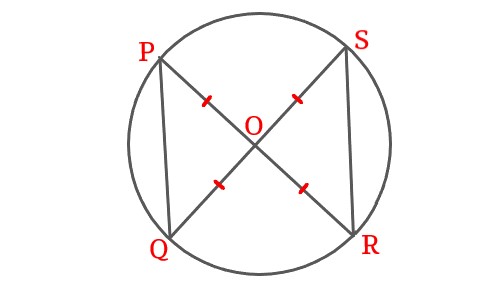
In the given figure AB and CD are intersecting at O, OA = OB and OC = OD, then prove that \$\triangleAOD \cong \triangleBOC\$.
|
Steps 2 |
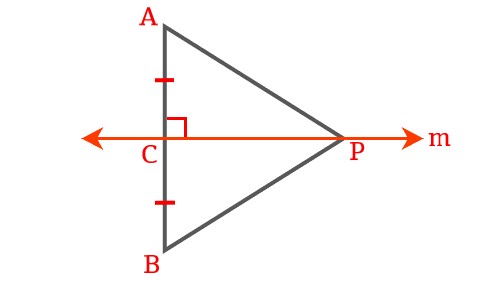
AB is a line segment and line m is its perpendicular bisector. If a point P lines on m, then show that P is eqidistant from A and B.
|
Steps 3 |
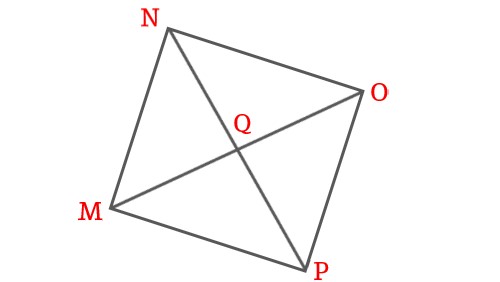
MNOP is a square, the diagonals of the square intersects at point Q. Then show that \$\triangle NQM \cong \triangle PQO\$.
|
Steps 4 |
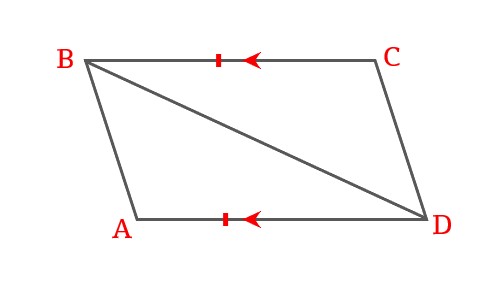
ABCD is a parallelogram, BD is the diagonal of parallelogram ABCD. Then show that \$\triangle CDB \cong \triangle ADB\$.
|
Steps 5 |
PR and QS are diameters of a circle with center O and PR is perpendicular to QS then show that \$\trianglePOQ \cong \triangle SOR\$.
|
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 26-November-2022 07:30 PM EST