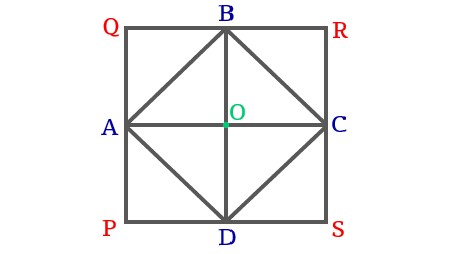
In the figur, PQRS is a square with four congruent sides A, B, C and D are the midpoints of PQ, QR, RS and SP and \$AC \bot BD\$. Prove that \$\triangle AOB \cong \triangle DOC\$.

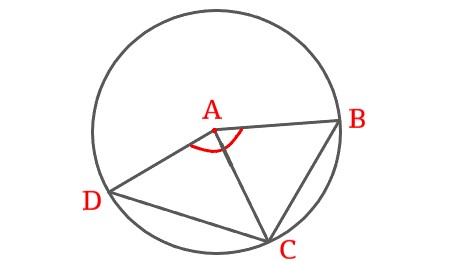
\$\angle BAC = \angle DAC\$, A is the center of the circle. Prove \$\triangle BAC \cong \triangle DAC\$.

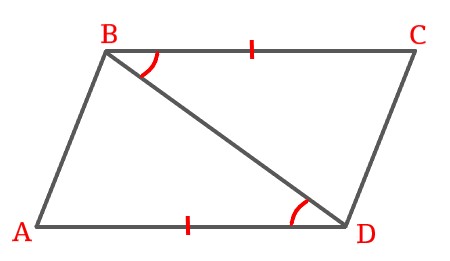
In a parallelogram ABCD BD is diagonal, \$\angle CBD = \angle ADB\$ and BC = DA. Then prove \$\triangle CBD \cong \triangle ADB\$.

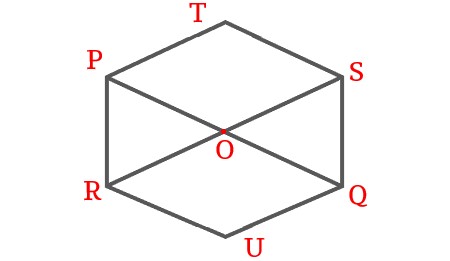
If O is the mid point of PQ and RS, prove \$\triangle PRO \cong \triangle QSO\$.

ABC is a isosceles right angled triangle right angled at B, D id the mid-point of hypotenues. Prove \$\triangle DBA \cong \triangle DBC\$.