Lesson Example Discussion Quiz: Class Homework |
Lesson |
Title: Area of 2D-Shapes |
Grade: 6-a Lesson: S4-L1 |
Explanation: Hello students; let us learn a new topic today with concepts, examples, and questions for you to solve. |
Lesson:
Definition: Square |
|
|
. |
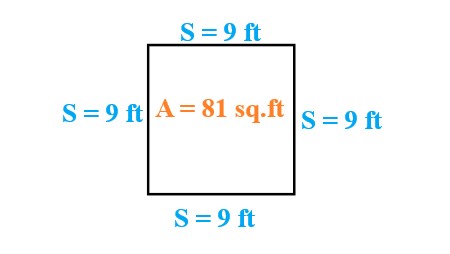
Explanation: The area of a square with each side 9 feet long is \$9 times 9\$ or 81 square feet (ft2). |
|
Definition: Rectangle |
|
|

. |
Explanation: In this image, the garden measures 30 meters in length and 8 meters in width , with a total perimeter of 76 meters. |
|
Definition: Triangle |
|
|
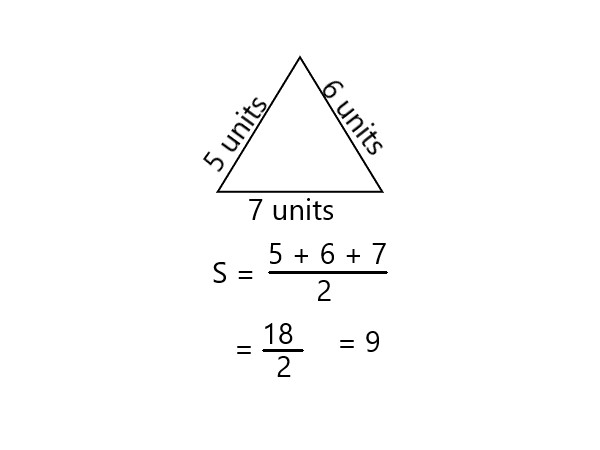
. |
Explanation: To find the area of a triangle with sides of length 5, 6, and 7 units, we can use Heron’s formula. First, we need to find the semi-perimeter, which is half of the perimeter, so we add up all three sides and divide by 2. In this case, the semi-perimeter is 9 units. Next, we can use Heron’s formula, which is:\$\sqrt(s(s−a)(s−b)(s−c))\$, then we get \$6\sqrt(6)\$ square units. |
|
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 13-February-2024 09:20AM EST