Step 1a

The side length of the equilateral triangle is 12 cm.

The formula for the area of an equilateral triangle: A = \$((\sqrt3)/4) a^2\$

Explanation: Equilateral triangle side length = 12 cm. Area formula: A = \$((sqrt(3))/4) a^2\$.

Step 1b

Now plug the values into the formula: A = \$((\sqrt3)/4) 12^2\$

A = \$((\sqrt 3)/4) 144\$

A = 62.352

So, the area of the equilateral triangle is 62.352 sq.meters.

Explanation: We can find the area of an equilateral triangle by using the formula A = \$(\sqrt3)/4 \times144\$. After plugging in the values, we get an area of 62.352 square meters.

Example: 2a

Given, the side of the square, s = 8 cm

Area of a Square = \$"side" \times "side"\$

Now plug the values into the formula : A = \$8 \times 8\$

A = 64 sq.cm

So, the area of a square is 64 sq.cm.

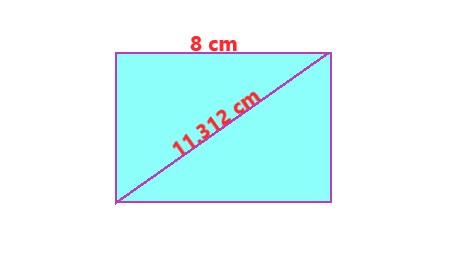
Explanation: In this step, we can calculate the area of a square with a side length of 8cm. The area of the square is 64 sq.cm.

Step 2b

Diagonal of a square formula: d = \$s\sqrt2\$ \$(∵ \sqrt 2 = 1.414)\$

Now plug the values into the formula : d = 8(1.414) = 11.312 cm.

So, the diagonal of a square is 11.312 cm.

Explanation: In this step, we can calculate the diagonal of a square with a side length of 8cm. The area of the square is 11.312 cm.