Lesson Example Discussion Quiz: Class Homework |
Lesson |
Title: Normal distribution |
Grade: 9-a Lesson: S4-L9 |
Explanation: Hello students, let us learn a new topic in statistics today with definitions, concepts, examples, and worksheets included. |
Lesson:
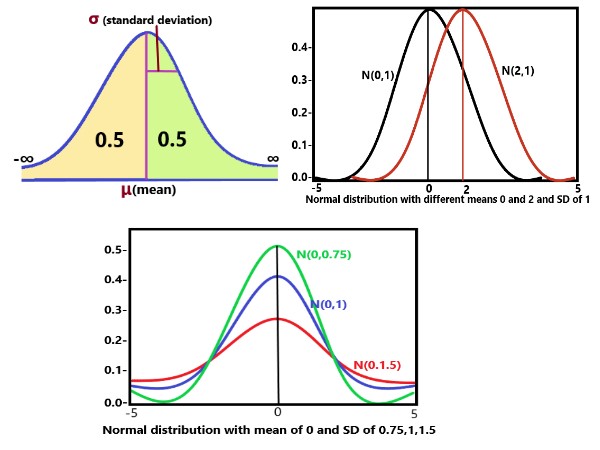
Definition: Normal distribution: |
|
|
|
Explanation: Properties of normal distribution:
|
|
Definition: Standard normal distribution: |
|
Every normal distribution is a version of the standard normal distribution that’s been stretched or squeezed and moved horizontally right or left. \$Z = (X-\mu )/ \sigma\$ X is random variable, \$\mu\$ = Mean , \$\sigma\$ = standard deviation Notation: X∼N(μ,σ) |
|
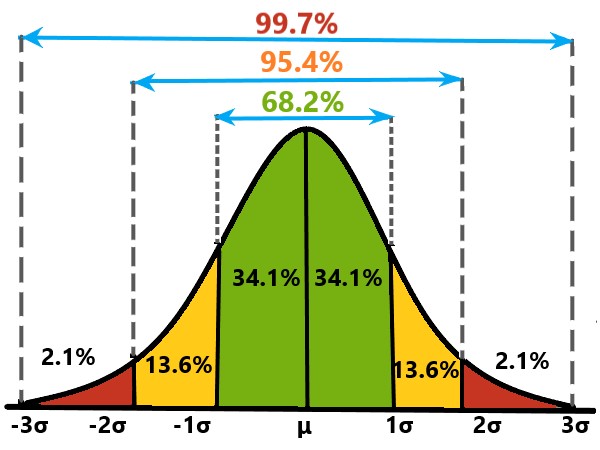
Explanation: Empirical rule:
|
|
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 27-February-2023 06:00 AM EST