SaiBook.us Statistics

Lesson Example Discussion Quiz: Class Homework

Lesson

Title: Probability distribution function of discrete random variable

Grade: 9-a Lesson: S4-L1

Explanation: Hello students, let us learn a new topic in statistics today with definitions, concepts, examples, and worksheets included.

Lesson:

Definition: Random variable:

A random variable is a type of variable in statistics whose possible values depend on the outcomes of a certain random phenomenon.
Since a random variable can take on different values, it is commonly labeled with a letter (e.g., variable “X”). Each variable possesses a specific probability distribution function.

$1$

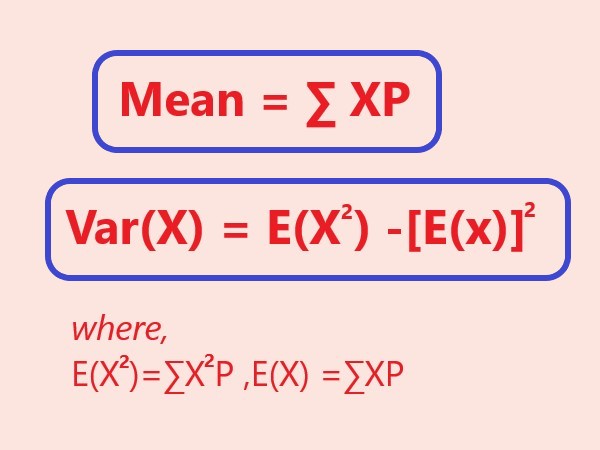
Explanation:

Random variable Formula:

Mean of random variable: X is the random variable,P is respective probabilites.

Variance of random variable: E(X) is Expectation of random variable,Variance is \$ \sigma^2\$

Definition: Types of random variable:

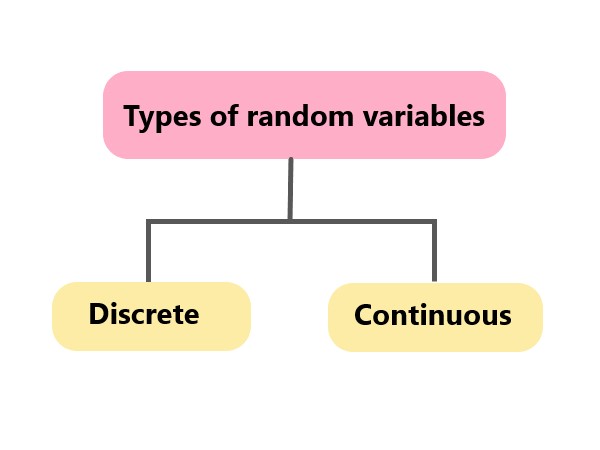
Types of random variables:

1.Discrete random variable: It is a variable whose values take only a finite number of values.Probability of outcome is equal to 1.

2.Continuous random variables: It can take infinite number of possible values.Probability of outcome is zero.

$2$

Explanation:

Example of discrete random variable:

Throwing a dice is purely random event,the dice can take only a finite number of outcome (1,2,3,4,5,6)

Example of continuous random variable:

Return of stocks is the best example.Return can take an infinite number of possible values(percentages).

Definition: Discrete random variable:

A discrete random variable is one which may take on only a countable number of distinct values such as 0,1,2,3,4,…….

A probability mass function is used to describe the probability distribution of a discrete random variable is a list of probabilities associated with each of its possible values.

$3$

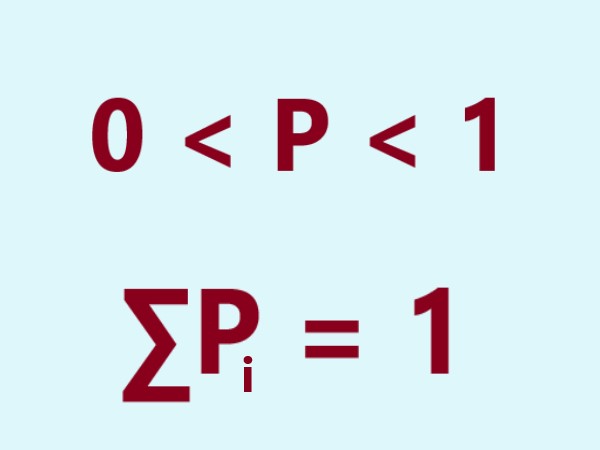
Explanation:

Suppose a random variable X may take n different values, with the probability that \$X = x_i\$ defined to be \$P(X = x_i) = p_i\$.

The probabilities \$p_i\$ must satisfy the following:

1: Each probability is between zero and one

2: Sum of the probabilities is one