Home Course Section

Register Enroll Refer

Lesson Example Discussion Quiz: Class Homework

Step-5

Title: Bowley’s Coefficient of skewness

Grade: 9-a Lesson: S2-L8

Explanation: Hello Students, time to practice and review the steps for the problem.

Lesson Steps

Step Type Explanation Answer

1

Problem

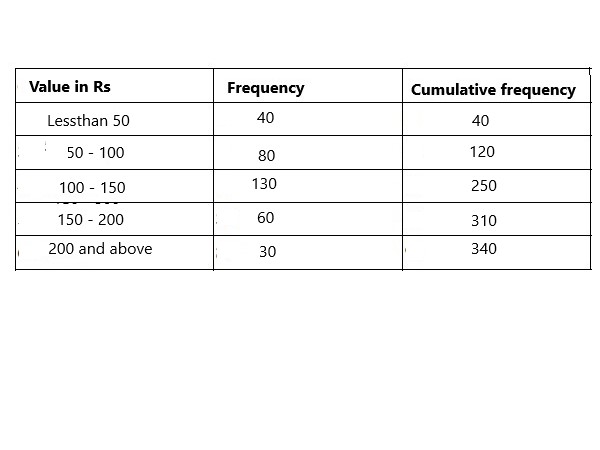
Find Bowley’s coefficient of skewness for the following data

2

Hint

To know the Bowley’s coefficient of skewness, we need to calculate three quartiles they are \$N / 4 , N / 2 ,(3N) / 4\$

3

Formula:

Bowley’s coefficient of skewness formula sk = \$(Q_3 + Q_1 - 2Q_2) / (Q_3 - Q_1)\$

4

Step

1

5

Step

Total frequency

N = 340

6

Step

class intervel

h = 50

7

Clue

First quartile Q_1 = \$"value of" (N/4)^(th) "observation"\$

8

Step

simplification of first quartile

\$Q_1\$ = \$340/4\$ = 85

9

Step

From the c.f \$85^(th)\$ observation is belongs to the class 50 - 100

10

Step

For the first quartile the frequency f = 80,
cumulative frequency of previous class CF = 40
and lower limit L = 50

11

Formula:

Formula for first quartile \$Q_1\$ = \$L + (h(N / 4 - CF)) / f\$

12

Step

simplification

\$Q_1\$ = \$50 + (50 (85 - 40)) / 80\$

13

Step

simplification

\$Q_1\$ = \$50 + (50 (45)) / 18\$

14

Step

simplification

\$Q_1\$ = \$50 + (2250) / 18\$

15

Step

simplification

\$Q_1\$ = \$50 + 125\$

16

Step

After simplification we get

\$Q_1\$ = 175

17

Clue

Second quartile \$Q_2\$ = \$"value of" (N/2)^(th) "observation"\$

18

Step

simplification of second quartile

\$Q_2\$ = \$340/2\$ = 170

19

Step

From the c.f \$170^(th)\$ observation is belongs to the class 100 - 150

20

Step

For the second quartile the frequency f = 130,
cumulative frequency of previous class CF = 120
and lower limit L = 100

21

Formula:

Formula for second quartile \$Q_2\$ = \$L + (h(N / 2 - CF)) / f\$

22

Step

simplification

\$Q_2\$ = \$100 + (50 (170 - 120)) / 130\$

23

Step

simplification

\$Q_2\$ = \$100 + (50 (50)) / 130\$

24

Step

simplification

\$Q_2\$ = \$100 + (2500) / 130\$

25

Step

simplification

\$Q_2\$ = \$100 + 19.23\$

26

Step

After simplification we get

\$Q_2\$ = 119.23

27

Clue

Third quartile \$Q_3\$ = \$"value of" ((3N)/4)^(th) "observation"\$

28

Step

simplification of third quartile

\$Q_3\$ = \$(3*340)/4\$ = 255

29

Step

From the c.f \$255^(th)\$ observation is belongs to the class 150 - 200

30

Step

For the third quartile the frequency f = 60,
cumulative frequency of previous class CF = 250
and lower limit L = 150

31

Formula:

Formula for third quartile \$Q_3\$ = \$L + (h((3N) / 4 - CF)) / f\$

32

Step

simplification

\$Q_3\$ = \$150 + (50 (255 - 250)) / 60\$

33

Step

simplification

\$Q_3\$ = \$150 + (50 (5)) / 60\$

34

Step

simplification

\$Q_3\$ = \$150 + (250) / 60\$

35

Step

simplification

\$Q_3\$ = \$150 + 4.16\$

36

Step

After simplification we get

\$Q_3\$ = 154.16

37

Formula:

Bowley’s coefficient of skewness formula sk = \$(Q_3 + Q_1 - 2Q_2) / (Q_3 - Q_1)\$

38

Step

simplification

sk = \$(154.16 + 175 - 2(119.23)) / (154.16 - 175)\$

39

Step

simplification

sk = \$(329.16 - 238.46) / -20.84\$

40

Step

After simplification we get

sk = -4.35

41

Answer

B

Tutor: Questions

Seq Type Question Audio

1

Problem

What did you learn from this problem?

2

Clue

What did you learn from the clues?

3

Hint

What did you learn from the Hints?

4

Step

What did you learn from the Steps?

5

Step

How can we improve the Steps?

Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 13-March-2023 06:00 AM EST

Tools: aws | angular | freepik | primeNG | saibook | vsc | asciidoctor | grammarly