SaiBook.us Statistics

Lesson Example Discussion Quiz: Class Homework

Lesson

Title: Bowley’s Coefficient of skewness

Grade: 9-a Lesson: S2-L8

Explanation: Hello students, let us learn a new topic in statistics today with definitions, concepts, examples, and worksheets included.

Lesson:

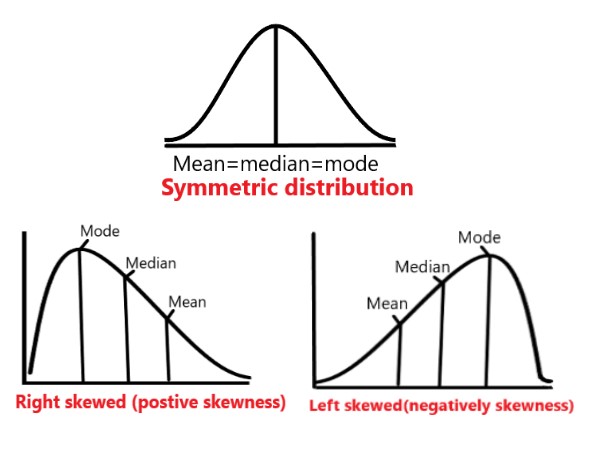
Definition: Skewness:

Skewness means lack of symmetry. We study skewness to have an idea about the shape of the curve drawn from the given data.
When the data set is not a symmetrical distribution, it is called a skewed distribution and such a distribution could either be positively skewed or negatively skewed.

$1$

Explanation:

The concept of skewness will be clear from the following three diagrams:

Symmetrical distribution: It is clear from the diagram below that in a symmetrical distribution the values of mean, median and mode coincide. The spread of the frequencies is the same on both sides of the centre point of the curve

Positively skewed distribution : If the mean exceeds the mode and median (Mode < Median < Mean) then the distribution is positively skewed. In other words, if the coefficient of skewness is positive then the distribution is skewed to the right.

Negatively skewed distribution: If the mode exceeds the median and mean (Mean < Median < Mode) then the distribution is negatively skewed. Thus, the coefficient of skewness will be negative and the distribution will be skewed to the left.

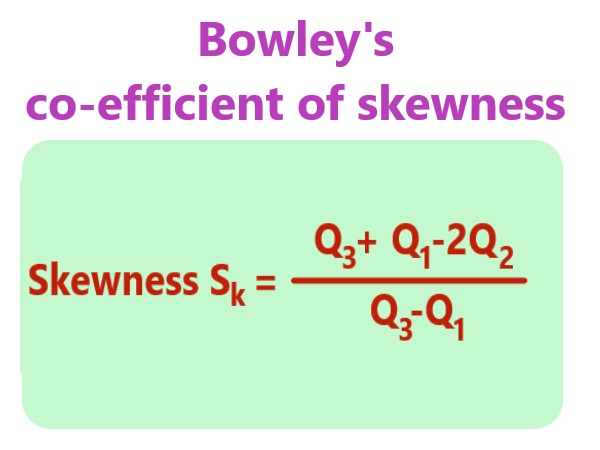
Definition: Bowley’s Coefficient of skewness:

Bowley skewness is a way to figure out if you have a positively-skewed or negatively skewed distribution.
Prof. Bowley has suggested a formula based on position of quartiles. In symmetric distribution quartiles will be equidistance from the median.

$2$

Explanation:

If skewness = 0,i.e,\$Q_3-Q_2 = Q_2-Q_1\$ then the distribution is symmetric or the curve is symmetrical.
If skewness < 0,i.e,\$Q_3-Q_2 < Q_2-Q_1\$ then the distribution or the curve is negatively skewed.
If skewness > 0,i.e,\$Q_3-Q_2 > Q_2-Q_1\$ then the distribution or the curve is positively skewed.
The formula for \$i^th\$ quartile is \$Q_i = ((i(N))/4)^(th)\$ value, i=1,2,3. where N is the total number of observations.