SaiBook.us SAT-3

Lesson Example Discussion Quiz: Class Homework

Example

Title: Statistics

Grade: Best-SAT3 Lesson: S8-P2

Explanation: The best way to understand SAT-3 is by looking at some examples. Take turns and read each example for easy understanding.

Examples:

Applying the IQR Method to Identify Outliers in Concert Ticket Prices.
Concert ticket prices: 75, 60, 80, 90, 65, 70, 85, 95, 70, and 100

Step 1a

75, 60, 80, 90, 65, 70, 85, 95, 70, and 100

Q1 (First Quartile) = 70
Q3 (Third Quartile) = 90
IQR = Q3 − Q1 = 90 − 70 = 20

\$"Lower Bound" = "Q"1 − 1.5 \times "IQR"\$
\$= 70 − 1.5 \times 20\$
\$= 70 − 30\$
\$ = 40 \$

\$"Upper Bound" = "Q"3 + 1.5 \times "IQR"\$
\$= 90 + 1.5 \times 20\$
\$= 90 + 30\$
\$ = 120\$

Explanation: Here, we find Lower bound and Upper bound and IQR.

Step 1b

Any data point below 40 or above 120 is considered an outlier.

In this dataset, all data points are within the bounds of 40 and 120.
There are no outliers in the given concert ticket prices using the IQR method, as all prices fall within the range of 40 to 120 dollars.

Explanation: Here, we identify outliers. There are no outliers in the given data.

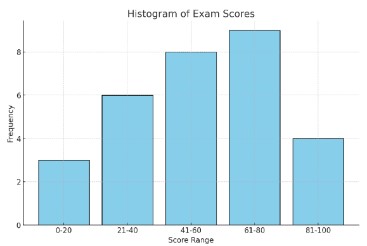
The following table represents the exam scores (out of 100) of 30 students in a class:

$3$

Create a histogram to represent the frequency distribution of the exam scores.

Step 2a

X-axis = Score range, Y-axis = Frequency
Drawbars for each score range, with the height of each bar corresponding to the frequency.

Explanation: Here, we draw the x-axis, and y-axis and drawbars to represent scores based on their frequency.

Step 2b

$3b$

Explanation: Therefore, the histogram provides a visual representation of the distribution of scores, making it easy to see which score ranges are most and least common in the class.