A quadratic equation is a polynomial equation of the second degree, meaning it has the highest exponent of 2. It is written in the general form:

\$"ax"^2 + "bx" + "c" = 0\$

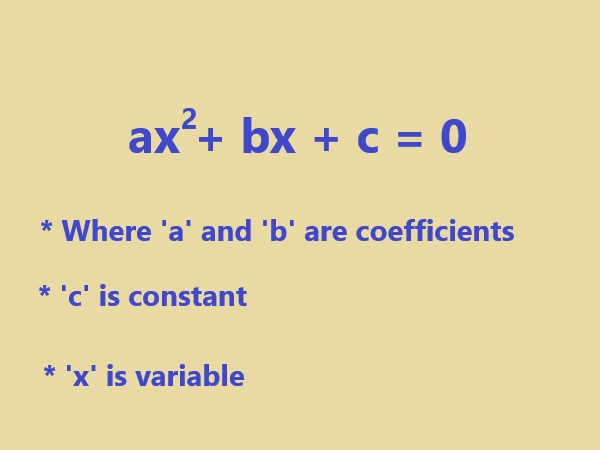
Explanation: Here the given image shows the where x represents the unknown variable, and a, b, are coefficients and c is constant.

Polynomial functions are mathematical functions that consist of variables raised to non-negative integer powers and multiplied by coefficients. They are expressed in the general form:

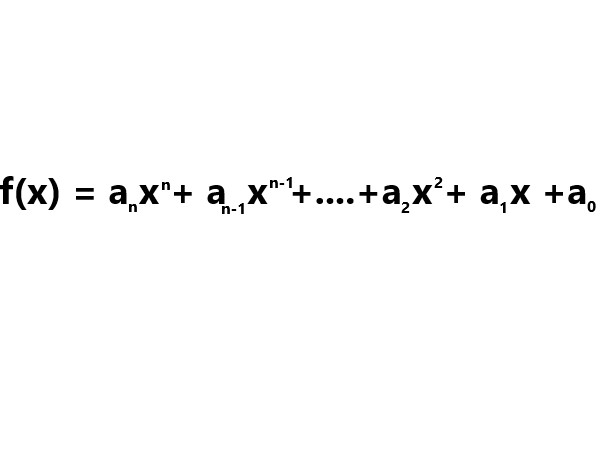
Explanation: Here is an image that shows how f(x) represents a function, where x is a variable, and a₀, a₁, …​, aₙ are the coefficients. The degree of the polynomial is determined by the highest power of x in the function.

A rational expression is an algebraic expression that represents a ratio or quotient of two polynomial expressions. It is essentially a fraction in which the numerator and denominator are polynomials.

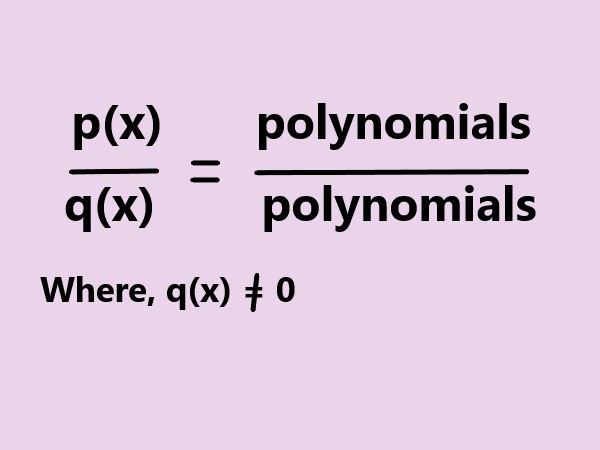
Explanation: Here the given image shows the rational expression of the form \$ (p(x))/(q(x)) = (polynomial)/(polynomial) \$
where \$ q(x) ne 0 \$.

A limit can be defined as the value that a function or sequence approaches as the input or index approaches a certain point. It represents the behavior or trend of the function or sequence near that particular point.

Explanation: Here, the given image shows the limit of a function of x equals A as and when x approaches a.

Continuity, in the context of mathematics and functions, refers to the smooth and unbroken nature of a function’s graph or behavior. It implies that there are no abrupt jumps, breaks, or holes in the graph of the function within a certain interval or over its entire domain.

More formally, a function f(x) is considered continuous at a point x = a if three conditions are satisfied.

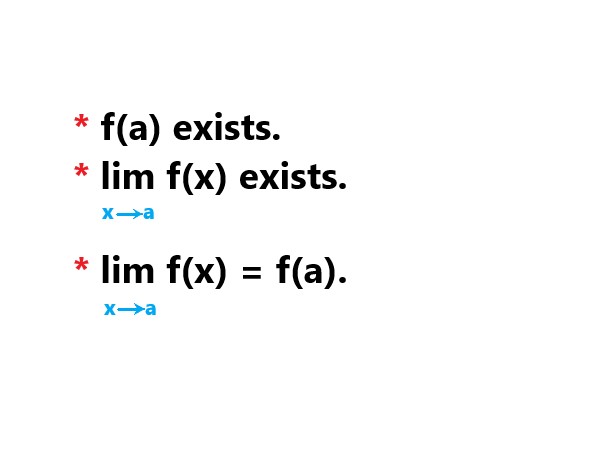
Explanation: Here, the given image shows the three conditions that are

If these conditions hold for every point in the domain of the function, then the function is said to be continuous over its entire domain.