SaiBook.us SAT-2

Lesson Example Discussion Quiz: Class Homework

Lesson

Title: Trigonometry Identities ( Pythagorean, reciporcal)

Grade: 1400-a Lesson: S3-L3

Explanation: Hello students, let us learn a new topic in SAT-2 today with definitions, concepts, examples, and worksheets included.

Lesson:

Definition: Trigonometry Identities

Trigonometric identities are equations that involve trigonometric functions and are true for every value of the variables within their domains.
Some common trigonometric identities include:
1. Pythagorean identities
2. Reciprocal identities

$1$

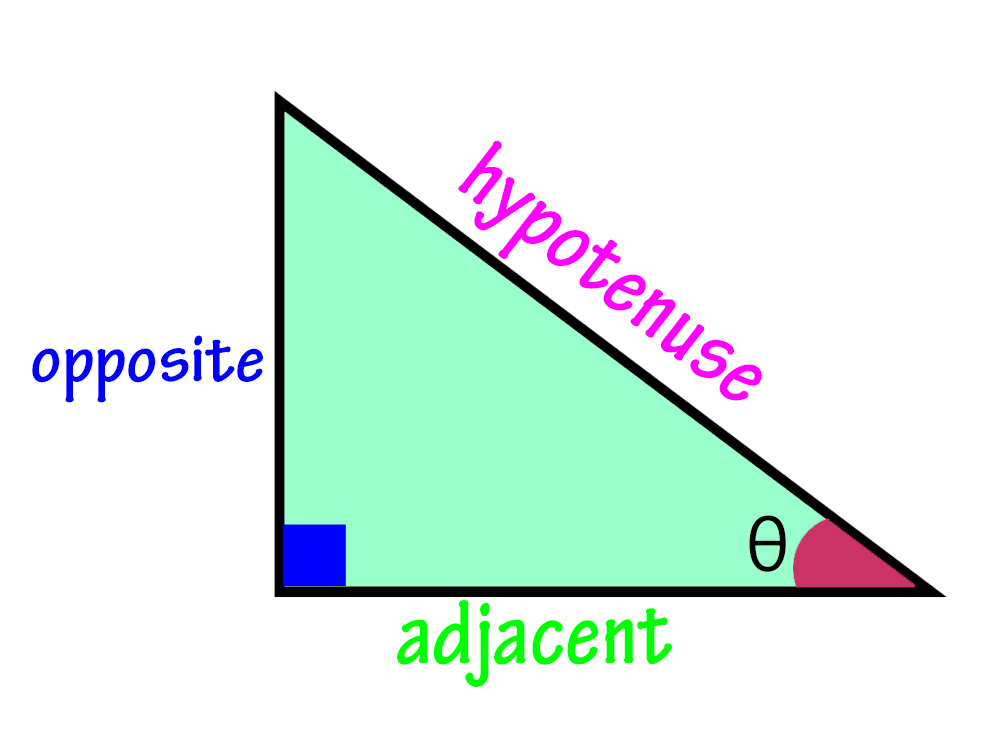
Explanation: In trigonometry, a right triangle contains a 90-degree angle. Its sides are designated based on their connection to this angle: the hypotenuse, opposite, and adjacent sides, each playing a distinct role.

Definition: Pythagorean identities

Pythagorean identities in trigonometry are a set of equations that relate the three basic trigonometric functions: sine (sin⁡), cosine (cos⁡), and tangent (tan⁡).

$2$

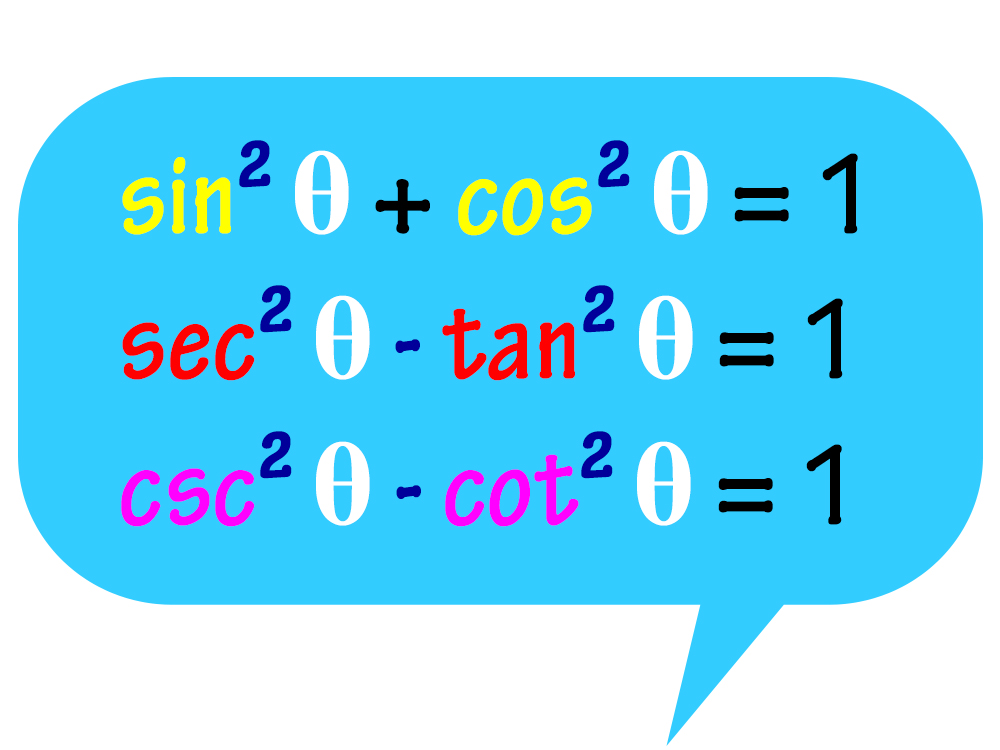
Explanation:

\$"sin"^2("x") + "cos"^2("x") = 1\$
\$1 + "tan"^2("x") = "sec"^2("x")\$
\$1 + "cot"^2("x") = "csc"^2("x")\$

Definition: Reciprocal identities

Reciprocal identities in trigonometry involve the reciprocals of the three primary trigonometric functions: sine (sin⁡), cosine (cos⁡), and tangent (tan⁡). These identities express the relationship between each trigonometric function and its reciprocal.

$3$

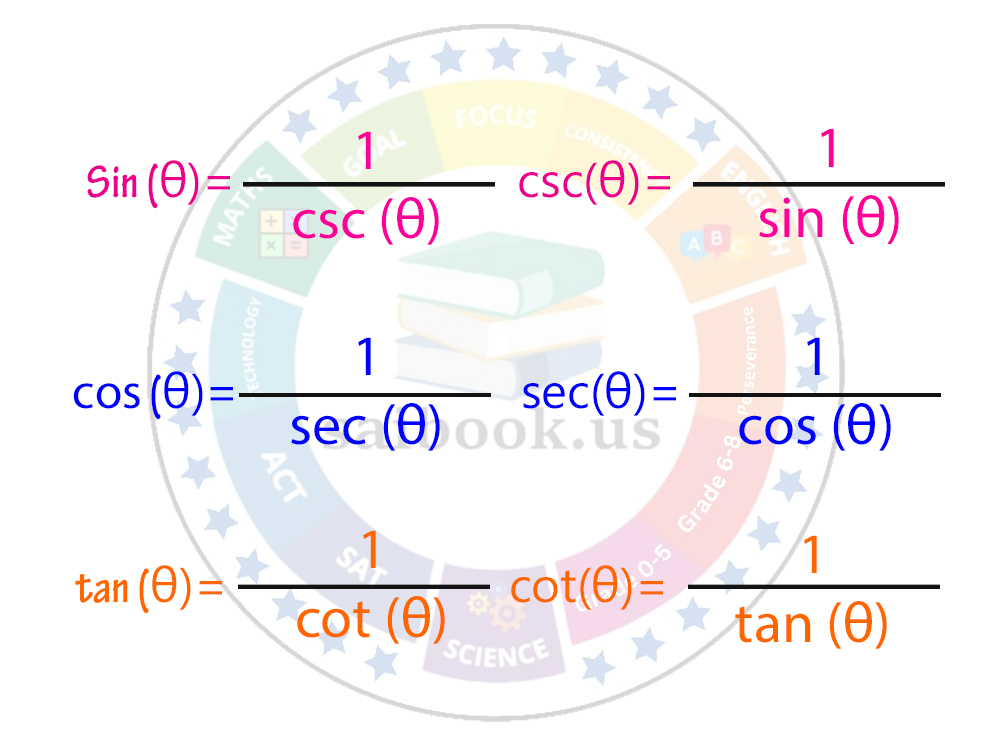
Explanation:

\$"csc"("x") = 1/("sin"("x"))\$
\$"sec"⁡("x") = 1/("cos"⁡("x"))\$
\$"cot"⁡("x") = 1/("tan"⁡("x"))\$