Lesson Example Discussion Quiz: Class Homework |
Quiz In Class |
Title: Slopes & Lines |
Grade: 1400-a Lesson: S3-L4 |
Explanation: Hello Students, time to practice and review. Let us take next 10-15 minutes to solve the ten problems using the Quiz Sheet. Then submit the quiz to get the score. This is a good exercise to check your understanding of the concepts. |
Quiz: in Class
| Problem Id | Problem | Options |
|---|---|---|
1 |
In triangle ABC, the measure of angle B is 90°, and \$\bar "BD"\$ is the altitude of the triangle. The length of \$\bar "AB"\$ is 30 and the length of \$\bar "AC"\$ is 28 greater than the length of \$\bar "AB"\$. What is the value of \$"BC" / "BD"\$? |
A) \$28/30\$ B) \$30/28\$ C) \$58/30\$ D) \$30/58\$ |
2 |
In triangle RST, angle T is a right angle, point L lies on \$\bar "RS"\$, point K lies on \$\bar "ST"\$, and \$\bar "LK"\$ is parallel to \$\bar "RT"\$. If the length of \$\bar "RT"\$ is 72 units, the length of \$\bar "LK"\$ is 24 units, and the area of triangle RST is 792 square units, what is the length of \$\bar "KT"\$, in units? |
A) \$33/3\$ B) \$22/3\$ C) \$3/44\$ D) \$44/3\$ |
3 |
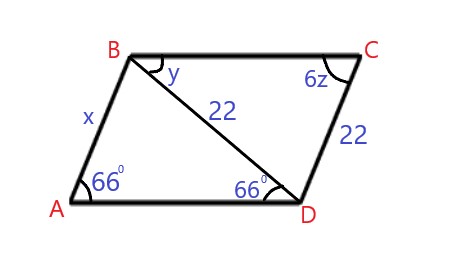
Find the values of x, y, and, z in the figure.
|
A) x = 24 y = 62 z = 12 B) x = 22 y = 66 z = 11 C) x = 22 y = 64 z = 11 D) x = 22 y = 64 z = 12 |
4 |
Find the shortest distance from the point (2, 3, 4) to the line passing through the points (1, 2, 0) and (-2, 1, 2). |
A) \$4/(\sqrt 14)\$ B) \$2/(\sqrt 14)\$ C) \$4/(\sqrt 7)\$ D) \$4/(\sqrt 5)\$ |
5 |
A line l1 passes through the point A(2,3) and is perpendicular to the line 2x−3y=5. Another line l2 passes through the point B(1,−2) and is perpendicular to l1 . Find the equation of l2 . |
A) y = \$2/3x - 8/3\$ B) y = \$2/5x - 8/3\$ C) y = \$2/3x - 8/5\$ D) y = \$3/2x - 8/3\$ |
6 |
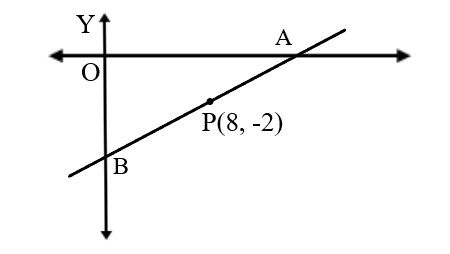
A line AB meets X - axis at A and Y - axis at B. P (8, -2) divides AB in the ratio 2 : 4. Find the equation of the line through P and perpendicular to AB.
|
A) 2x + y -7 = 0 B) 2x + y -14 = 0 C) 2x + 3y -14 = 0 D) 2x + y + 14 = 0 |
7 |
The triangle formed by the lines x + 2y = 1, 3x + 2y – 4 = 0 and x – y + 1 = 0 lies in which quardinate. |
A) \$3^"rd" " quardinate"\$ B) \$2^"nd" " quardinate"\$ C) \$4^"th" " quardinate"\$ D) \$1^"st" " quardinate"\$ |
8 |
The slope of the normal to the curve \$y = 2x^2 - 4\$ at P(1, -2) is |
A) \$1/4\$ B) \$4\$ C) \$-1/4\$ D) \$-4\$ |
9 |
Find the value of 'P' for which lines (-P )x + y - 4 = 0 and ( 4 + P)x - 4y + 6 = 0 are perpendicular? |
A) 4 B) 2 C) -2 D) -4 |
10 |
Find the value of x such that the lines through the points (8, -6) and (10, x) is perpendicular to the line through the points (5, 3) and (6, - 4)? |
A) \$83/7\$ B) \$82/7\$ C) \$-82/9\$ D) \$-82/7\$ |
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 20-May-2024 09:20AM EST