SaiBook.us SAT-1

Lesson Example Discussion Quiz: Class Homework

Lesson

Title: Slopes & Lines

Grade: 1400-a Lesson: S3-L4

Explanation: Hello Students, time to learn definitions. Let us take turns and read definitions and explain the pictures. Try to remember or memorize the definitions. Pay special attention to the pictures and communicate in your own words.

Lesson:

Definition: Slope of a Line

The slope of a line is a measure of its steepness and direction.

It is defined as the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line.

This ratio is usually represented by the letter m.

Mathematically, if the line passes through points(x1, y1) & (x2, y2), the slope m is given by:
m = \$(y2 - y1)/(x2 - x1)\$

$1$

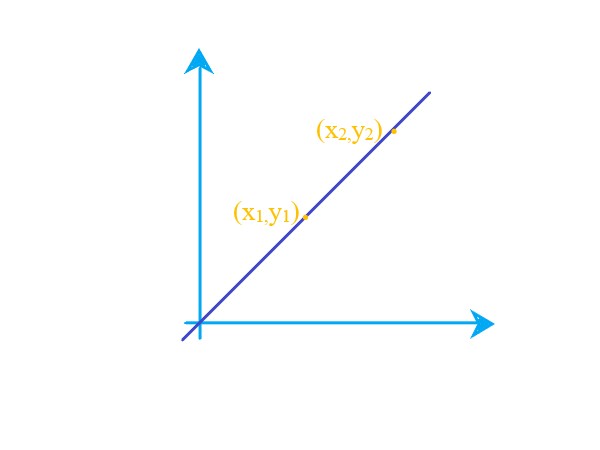
Explanation: In this image, the slope of the line passing through the points(3, -4) & (7, 10) is m = 3/2 by using m = \$(y2 - y1)/(x2 - x1)\$.

Definition: Lines

The most common form of the equation of a line is the slope-intercept form:
y = mx + c where 𝑚 is the slope of the line and 𝑏 is the y-intercept (the point where the line crosses the y-axis).

Another form is the point-slope form, which is useful if you know a point on the line(x1, y1) and the slope m: y - y1 = m(x - x1).

Perpendicular lines intersect at right angles. Their slopes, denoted as 𝑚1 and m2, satisfy the relationship 𝑚1×𝑚2 = −1.

Parallel lines intersect at right angles. Their slopes, denoted as 𝑚1 and m2, satisfy the relationship 𝑚1 = 𝑚2.

The distance between two lines is d = \$(c2- c1)/\sqrt(a^2 + b^2)\$

Normal form of equation of line is x cos ω + y sin ω = p.

$2$

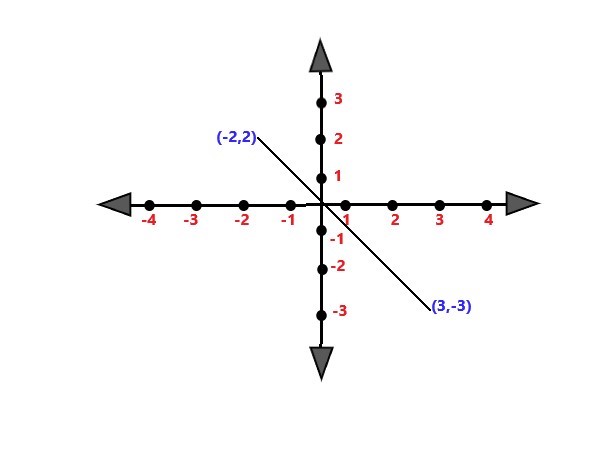
Explanation: In this image, the equation of the line that passes through the point (2,−1) with a slope of 4 is y = 4x - 9.