SaiBook.us Geometry

Lesson Example Discussion Quiz: Class Homework

Example

Title: Angles

Grade: 6-a Lesson: S2-L4

Explanation: The best way to understand geometry is by looking at some examples. Take turns and read each example for easy understanding.

Examples:

Find ∠BAC and ∠ABC.

Step 1a

150º is an exterior angle of the Δ ABC. So, by using the exterior angle theorem, we have, ∠BAC + ∠ABC = 150º.

$1a$

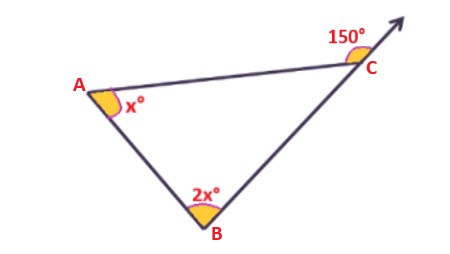
Explanation: Using the exterior angle theorem, we can calculate that the sum of angles BAC and ABC equals 150º. Since 150º is an exterior angle of ΔABC.

Step 1b

x + 2x = 150º

After addition we get 3x = 150º

Explanation: The equation x + 2x = 150°, which simplifies to 3x = 150°.

Step 1c

Divide 3 on both sides. ⇒ \$(3x)/3 = (150º)/3\$

⇒ x = 50º

Therefore, ∠BAC = x = 50º and ∠ABC = 2xº = 100º.

Explanation: After simplification, ∠BAC is x = 50º and ∠ABC is 2xº = 100º.

Find the area and the perimeter of a rhombus whose diagonal measures are 4 cm and 8 cm and side measure is 9 cm.

Step 2a

The length of one diagonal is given (d1) 4 cm and the second diagonal(d2) is 8 cm.

$2a$

Explanation: The length of the two diagonals are given as 4 cm and 8 cm, respectively.

Step 2b

Area (A) of a rhombus can be calculated using the formula: A = \$(d1 \times d2)/2\$.

Explanation: To calculate the area of a rhombus, multiply the lengths of its diagonals and divide the result by 2. The formula is A = \$(d1 \times d2)/2\$.

Step 2c

Now plug the values into the formula: A = \$(4 \times 8)/2\$ = \$32/2\$ = 16 \$cm^2\$

Explanation: Now, we can substitute the given values in the formula: A = \$(4 \times 8)/2\$ = \$16 cm^2\$.

Step 2d

The length of one side of a rhombus is 9 cm.

The perimeter of the rhombus formula is : P = 4s

Now plug the values into the formula: P = 4(9) = 36 cm

Explanation: In this step, we need to find the length of the perimeter of a rhombus using a formula. Then we get 36 cm.