Adding and subtracting polynomials involves combining or separating terms with similar variables and their corresponding coefficients. To add or subtract polynomials, align like terms (those with the same variable and exponent) and perform the arithmetic operations (addition or subtraction) on their coefficients.

Explanation: The given image shows the Addition and Subtraction between the polynomials.

Multiplying polynomials involves taking two or more polynomials and finding their product. A polynomial is an algebraic expression consisting of variables and coefficients, combined using addition, subtraction, and multiplication, but not division or exponentiation with non-negative integer exponents.

To multiply polynomials, you distribute each term of one polynomial across each term of the other polynomial(s), then combine like terms and simplify the resulting expression.

Explanation: For example, if you have two polynomials (a + b)(a + b) and (c + d)(c + d), you would multiply each term in the first polynomial by each term in the second polynomial: (a+b)(c+d) = ac + ad + bc + bd

Dividing polynomials is the process of dividing one polynomial by another. There are two common methods: long division and synthetic division. Long division resembles the division of numbers, while synthetic division is a shorthand method for dividing by linear factors.

Both methods aim to find the quotient polynomial and, if applicable, the remainder polynomial.

Explanation: The image displays two ways of dividing polynomials: long division (left) and synthetic division (right). Both methods divide a polynomial (dividend) by another polynomial (divisor). However, synthetic division is a faster method for specific cases.

Synthetic division is a streamlined method for dividing polynomials, typically used when dividing by a linear term like (x − a). It’s faster and simpler than long division, involving only the coefficients of the polynomial and the given root. This approach employs arithmetic operations to quickly compute the quotient and remainder.

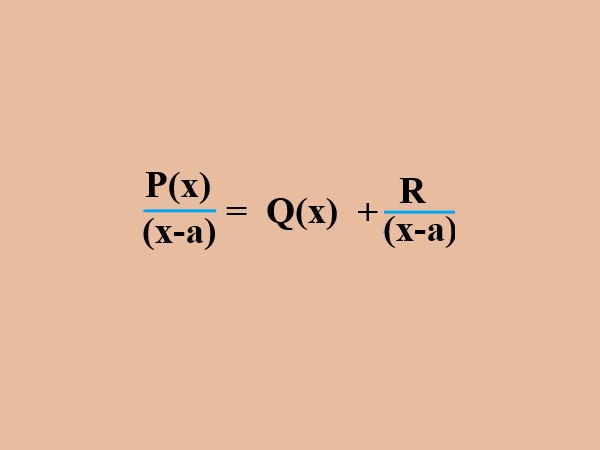
Explanation: This image shows the use of synthetic division to divide the polynomial P(x) by the linear divisor (x - a) to obtain a quotient Q(x) and a remainder R.