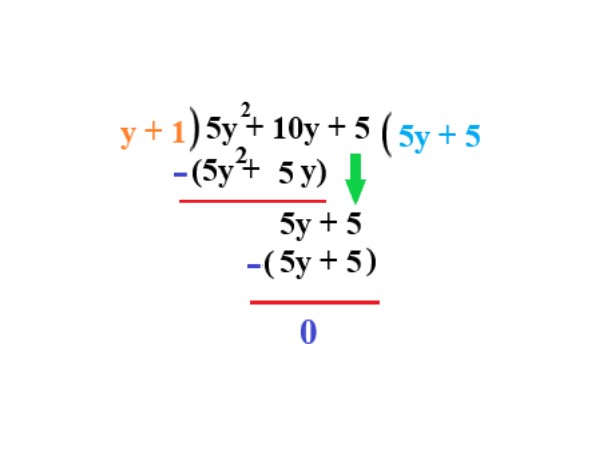SaiBook.us Algebra

Lesson Example Discussion Quiz: Class Homework

Example

Title: Test1

Grade: 8-b Lesson: S1-P1

Explanation: The best way to understand algebra is by looking at some examples. Take turns and read each example for easy understanding.

Examples:

Find the product of \$(2x^2−3x+1)\$ and (3x+2).

Step 1a

The given polynomial \$(2x^2 − 3x + 1)\$ and (3x + 2)

Let’s start multiplying:

\$2x^2\$ multiplied by 3x: \$2x^2 times 3x\$ = \$6x^3\$
\$2x^2\$ multiplied by 2: \$2x^2 times 2\$ = \$4x^2\$
− 3x multiplied by 3x: \$-3x times 3x \$ = \$ - 9x^2\$
- 3x multiplied by 2: \$-3x times 2\$ = - 6x
1 multiplied by 3x: \$1 times 3x\$ = 3x
1 multiplied by 2: \$ 2 times 1\$ = 2

Explanation: This involves multiplying every term in the polynomial by each term in the polynomial expression to expand it fully.

Step 1b

Now, let’s add up all the results:
\$6x^3 + 4x^2 - 9x^2 - 6x +3x +2\$
Combining like terms:
\$6x^3 − 5x^2 − 3x + 2\$
So, the product of \$(2x^2 − 3x + 1)\$ and (3x+2) is \$6x^3 − 5x^2 − 3x + 2\$.

Explanation: Multiply each term, sum the products, and then consolidate terms for the final result.

Divide the polynomial \$ 5y^2 + 10y + 5 \$ by \$ y + 1 \$.

Step 2a

$1$

Explanation:

To divide \$5y^2+10y+5\$ by y + 1, first divide \$5y^2\$ by y, which equals 5y. Write it on the top line.
Multiply y + 1 by 5y, which equals \$5y^2+5y\$. Write it below the dividend.
Subtract \$5y^2+5y\$ from \$5y^2+10y+5\$, getting 5y. Bring down 5 and repeat the process.
Divide 5y by y, which equals 5. Write it next to the previous quotient term.
Multiply y + 1 by 5, which equals 5y + 5. Write it below the previous product. Subtract 5y + 5 from 5y, getting 0.
The quotient is 5y + 5, which is the result of dividing \$5y^2+10y+5\$ by y + 1 with no remainder.