SaiBook.us WordProblems

Home Course Section

Register Enroll Refer

Lesson Example Discussion Quiz: Class Homework

Example

Title: Triangles

Grade: 8-a Lesson: S4-L1

Explanation: Here are some examples of the topic with images and steps in sequence.

Examples:

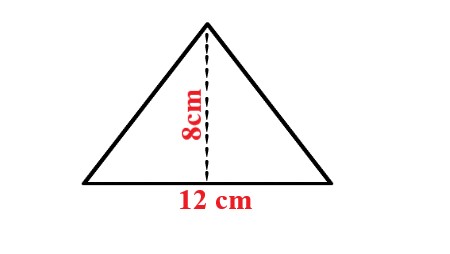
Example: 1a

Find the area of a triangle whose altitude and base are 12 cm and 8 cm, respectively.

Base of triangle = 8 cm
Height of triangle = 12 cm
Area of triangle = ½ × base × height
```
= ½ × 8 × 12 = 48 cm2.
```

Explanation: In the given problem, the base of triangle is 8 cm and the height of triangle is 12 cm. By using the formula Area of triangle = ½ × base × height, the area of the triangle is 48 cm2.

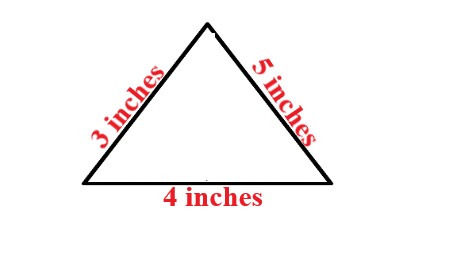
Example: 2a

Find the area of a triangle whose length of each side is 3 inches, 5 inches and 4 inches.

Let a = 3 inches, b = 5 inches, c = 4 inches
The semi perimeter of a triangle, s = \$(a + b + c)/(2)\$ = \$(3 + 4 + 5)/2\$ = \$12/2\$ = 6 inches.

Area of triangle = √[s(s – a)(s – b)(s – c)]

= √[6 × (6 – 3) × (6 – 4) × (6 – 5)]

= √[6 × 3 × 2 × 1]

= √36 = 6 sq. inches.

Explanation: In the given problem, let a = 3 inches, b = 5 inches, c = 4 inches and the semi perimeter of a triangle is 6 inches. By using Area of triangle = √[s(s – a)(s – b)(s – c)], the area of triangle is 6 sq. inches.

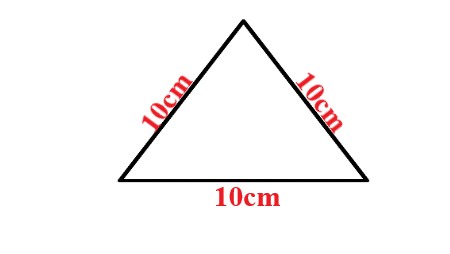
Example: 3a

Find the perimeter of a triangle whose each side is 10 cm.

Since all three sides are equal in length, the triangle is an equilateral triangle i.e. a = b = c = 10 cm
Perimeter of a triangle = a + b + c = 10 + 10 + 10 = 30cm.

Explanation: In the given problem, since all three sides are equal in length, the triangle is an equilateral triangle i.e. a = b = c = 10 cm. Therefore, the perimeter of a triangle = a + b + c = 10 + 10 + 10 = 30cm