Lesson Example Discussion Quiz: Class Homework |
Lesson |
Title: Three-dimensional (3D) shapes |
Grade: 6-a Lesson: S4-L2 |
Explanation: Hello students; let us learn a new topic today with concepts, examples, and questions for you to solve. |
Lesson:
Definition: Cylinder |
|
|
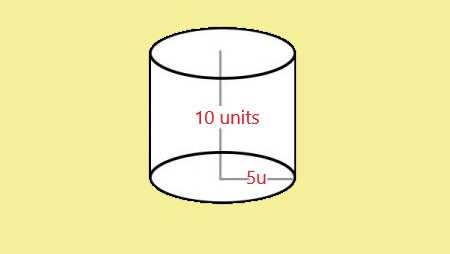
. |
Explanation: In this image, the cylinder has a surface area of 471.24 square units. The cylinder has a radius of 5 units and a height of 10 units. The formula used to calculate the surface area is A = 2πr² + 2πrh. |
|
Definition: Cone |
|
|
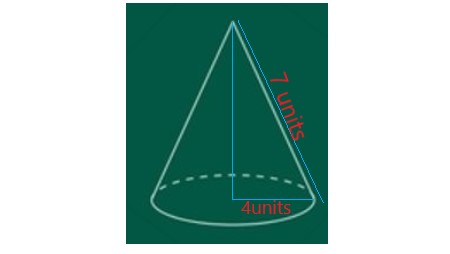
. |
Explanation: The cone in this example has a surface area of 138.23 sq. units with radius 4 units and slant height 7 units (A = πr(r + l), π = 3.141). |
|
Definition: Cube |
|
|
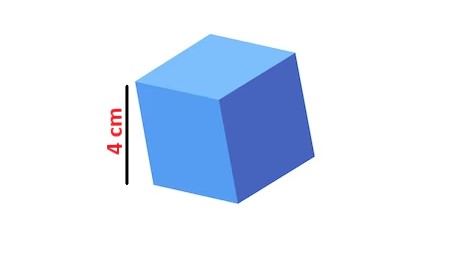
. |
Explanation: In this image, the cube has a side length of 4 cm and a surface area of \$96 cm^2\$. |
|
Definition: Cuboid |
|
|
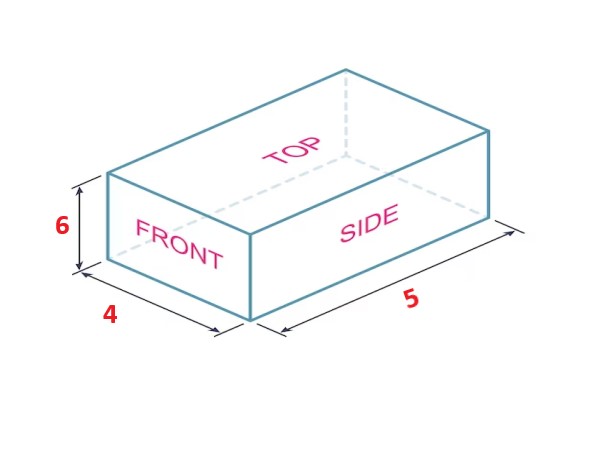
. |
Explanation: In this image, the cuboid has a surface area of 148 square centimeters with the given dimensions. (Surface Area = 2lw + 2lh + 2wh, where l = 6, w = 4, and h = 5.) |
|
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 13-February-2024 09:20AM EST