SaiBook.us Statistics

Lesson Example Discussion Quiz: Class Homework

Lesson

Title: Continuous random variable

Grade: 9-a Lesson: S4-L7

Explanation: Hello students, let us learn a new topic in statistics today with definitions, concepts, examples, and worksheets included.

Lesson:

Definition: Random variable:

A random variable is a type of variable in statistics whose possible values depend on the outcomes of a certain random phenomenon.
Since a random variable can take on different values, it is commonly labeled with a letter (e.g., variable “X”). Each variable possesses a specific probability distribution function.

$1$

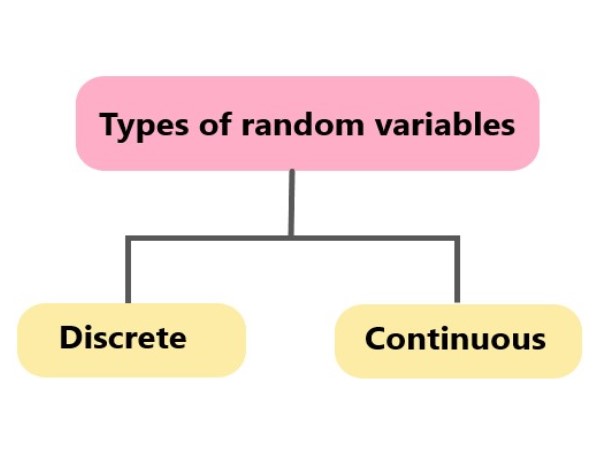
Explanation:

Types of random variables:

1.Discrete random variable: It is a variable whose values take only a finite number of values.Probability of outcome is equal to 1.

2.Continuous random variables: It can take infinite number of possible values.Probability of outcome is zero.

Definition: Continous random variable:

A continuous random variable can be defined as a random variable that can take on an infinite number of possible values. Due to this, the probability that a continuous random variable will take on an exact value is 0.
The cumulative distribution function and the probability density function are used to describe the characteristics of a continuous random variable.

$2$

Explanation:

PDF of Continuous Random Variable:

The probability density function of a continuous random variable can be defined as a function that gives the probability that the value of the random variable will fall between a range of values

F(x) is the cumulative distribution function.

The PDF has to satisfy the following conditions:
1.\$\int_-\infty^(+\infty)\$f(x)dx = 1
2.\$f(x)≥0\$

CDF of Continuous Random Variable:

The cumulative distribution function of a continuous random variable can be determined by integrating the probability density function.

It can be defined as the probability that the random variable, X, will take on a value that is lesser than or equal to a particular value, x

Definition: Mean and variance of random variable:

Mean of Continuous Random Variable:

The mean of a continuous random variable can be defined as the weighted average value of the random variable, X.

It is also known as the expectation of the continuous random variable

Variance of Continuous Random Variable:

The variance of a continuous random variable can be defined as the expectation of the squared differences from the mean.

It helps to determine the dispersion in the distribution of the continuous random variable with respect to the mean

$3$

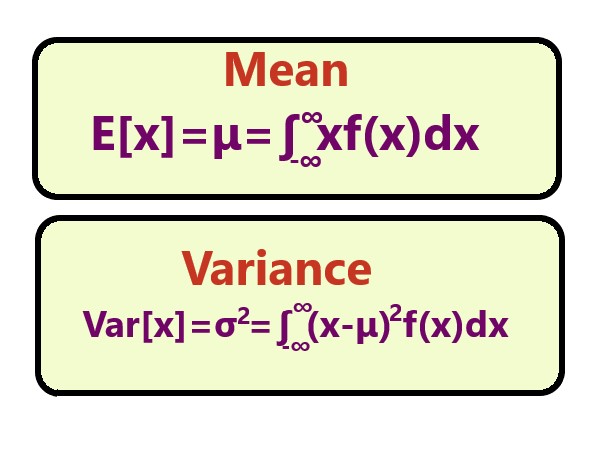
Explanation:

Types of Continuous random variable:

Uniform random variable
Normal random variable
Expotential random variable