Lesson Example Discussion Quiz: Class Homework |
Lesson |
Title: Geometric distribution |
Grade: 9-a Lesson: S4-L6 |
Explanation: Hello students, let us learn a new topic in statistics today with definitions, concepts, examples, and worksheets included. |
Lesson:
Definition: Geometric distribution: |
|
n = number of experiments, p = Probability of success in any experiment, q= Probability of failures in any experiment, x = number of successful trials. Notation: X ∼ G(p) |

|
Explanation: Applications of binomial distribution:
|
|
Definition: Mean and variance of geometric distribution: |
|
|
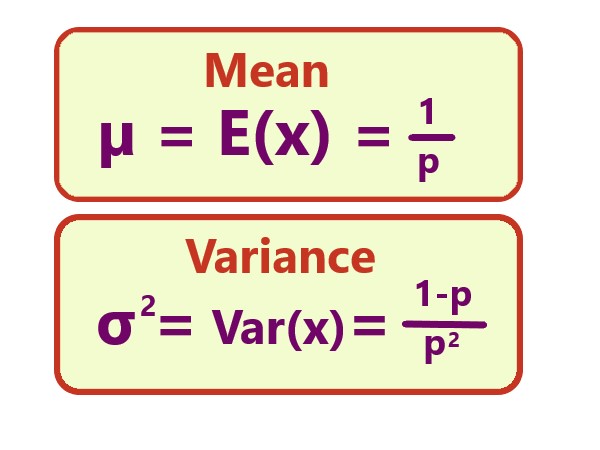
|
Explanation: Properties of Binomial Distribution:
|
|
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 27-February-2023 06:00 AM EST