Terms related to Baye’s theorem:

Conditional probabilty: It is the probability of an event A is based on the occurance of another event.

Sample space: The sample space is the set of all possible outcomes of an event

Hypothesis: The events \$E_1,E_2,....,E_n\$ is called the hypothesis.

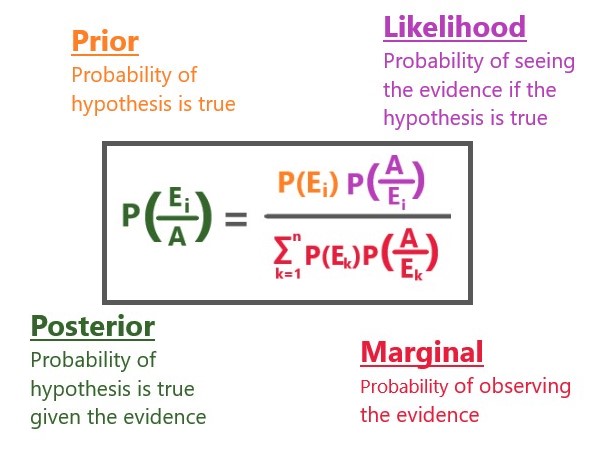
Explanation:

Statement: Let \$E_1,E_2,....,E_n\$ be a set of events associated with a sample space S, where all the events \$E_1,E_2,....,E_n\$ have non-zero probability of occurrence and they form a partition of S. Let A be any event associated with S, then according to baye’s theorem

\$P(E_i/A) = (P(E_i)P(A/E_i))/(\sum_{k=1}^n P(E_k)P(A/E_k))\$

for any k = 1, 2, 3, …., n

Proof:

Let us express A in terms of \$E_i\$ i.e,\$E_1,E_2,....,E_n\$ are in sample space S.

A = A ∩ S ⇒ A = A ∩ \$E_1,E_2,....,E_n\$

A = \$(A ∩E_1)∪(A ∩E_2)∪....∪(A ∩E_n)\$

Apply probability on both the sides

P(A) = \$P((A ∩E_1)∪(A ∩E_2)∪....∪(A ∩E_n))\$

we know (A∪B) = P(A)+P(B)

Then,P(A) = \$P((A ∩E_1)P(A ∩E_2)....+P(A ∩E_n))\$

According to the multiplication theorem of a dependent event,

P(A∩B) = P(A)P(B/A)

P(A) = \$P(E_1)P(A/E_1) + P(E_2)P(A/E_2) +.....+P(E_n)P(A/E_n)\$

Total probability of P(A) = \$\sum_{k=1}^n P(E_k)P(A/E_k)\$ ⇒equation(1)

According to the conditional probability formula,

\$P(E_i/A) = (P(E_i ∩ A))/(P(A))\$,i=1,2,…​n ⇒equation(2)

using the formula for conditional probability formula of \$P(A/E_i)\$,

\$P(E_i ∩ A) = P(E_i)P(A/E_i)\$ ⇒equation(3)

Substitute equation(1) and (3) in (2),we get

\$P(E_i/A) = (P(E_i)P(A/E_i))/(\sum_{k=1}^n P(E_k)P(A/E_k))\$

Hence,Baye’s theorem is proved