SaiBook.us Statistics

Lesson Example Discussion Quiz: Class Homework

Lesson

Title: Kurtosis

Grade: 9-a Lesson: S2-L9

Explanation: Hello students, let us learn a new topic in statistics today with definitions, concepts, examples, and worksheets included.

Lesson:

Definition: Kurtosis:

Kurtosis is a measure of the tailedness of a distribution. Tailedness is how often outliers occur. Excess kurtosis is the tailedness of a distribution relative to a normal distribution.
Tails are the tapering ends on either side of a distribution. They represent the probability or frequency of values that are extremely high or low compared to the mean. In other words, tails represent how often outliers occur.
Skewness essentially measures the symmetry of the distribution, while kurtosis determines the heaviness of the distribution tails.

Kurtosis = \$(\sum(x_i - \barx)^4)/(n×\sigma^4) \$

where \$\barx\$ = mean ,
Standard deviation\$(\sigma) = \sqrt((\sum(x_i - \barx)^2)/n)\$

$1$

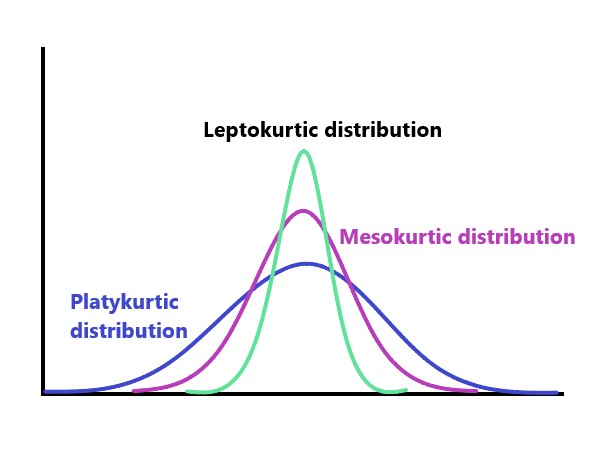
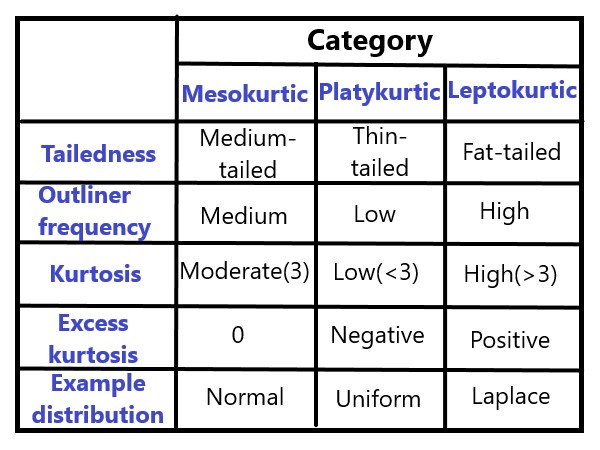
Explanation:

Types of kurtosis :

Mesokurtic: Data that follows a mesokurtic distribution shows an excess kurtosis of zero or close to zero. This means that if the data follows a normal distribution, it follows a mesokurtic distribution.

Leptokurtic: Leptokurtic indicates a positive excess kurtosis. The leptokurtic distribution shows heavy tails on either side, indicating large outliers.

Platykurtic: A platykurtic distribution shows a negative excess kurtosis. The kurtosis reveals a distribution with flat tails. The flat tails indicate the small outliers in a distribution

If \$\gamma_2=0\$ i.e,\$\beta_2=3\$,the distribution is mesokurtic.
If \$\gamma_2>0\$ i.e,\$\beta_2>3\$,the distribution is leptokurtic.
If \$\gamma_2<0\$ i.e,\$\beta_2<3\$,the distribution is platykurtic.

For moments,

\$µ_1 = µ'_1 - µ'_1\$
\$µ_2 = µ'_2 - (µ'_1)^2\$
\$µ_3 = µ'_3 - 3(µ'_2)(µ'_1) +2(µ'_1)^3\$
\$µ_4 = µ'_4 - 4(µ'_1)(µ'_3) +6(µ'_2)(µ'_1)^2 -3(µ'_1)^4\$
Skewness \$\beta_1 = µ_3^2/µ_2^3\$
Kurtosis \$\beta_2 = µ_4/µ_2^2\$

$2$