SaiBook.us Statistics

Example

Title: Measures of variation- Sample Standard deviation

Grade: 9-a Lesson: S2-L3

Explanation: The best way to understand statistics is by looking at some examples. Take turns and read each example for easy understanding.

Examples:

Find the standard deviation of the following samples 2,3,6,6,8.

Step 1a

Find the mean

Explanation: Let us add all the scores and divide by total number of scores

\$\barX\$ = \$(2+3+6+6+8)/(5)\$ = \$25/5\$ = 5

Step 1b

subtracting each score from mean and square each deviation

Explanation:

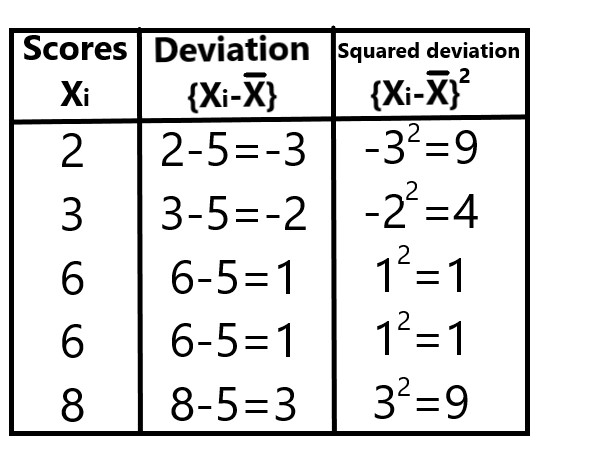
score \$X_i\$ ⇒ Deviation \${X_i - \barX}\$

squared deviation \${X_i - \barX}^2\$

2 ⇒ 2-5 = -3

\$(-3)^2\$ = 9

3 ⇒ 3-5 = -2

\$(-2)^2\$ =4

6 ⇒ 6-5 = 1

\$(1)^2\$ =1

6 ⇒ 6-5 = 1

\$(1)^2\$ =1

8 ⇒ 8-5 = 3

\$(3)^2\$ = 9

$1$

Step 1c

Calculate the Sample standard deviation.

Explanation: Add the squared deviation \${X_i - \barX}^2\$ = 9 + 4 + 1 + 1 + 9 = 24

Divide the sum by number of scores to get the variance \$frac\{24}{5-1}\$ = \$frac\{24}{4}\$ = 6

Take the square root of the squared deviation (or) variance \$\sqrt(6)\$ \$\approx\$ 2.449

Population standard deviation \$s\$ = 2.449