Quiz In Class |
|
Title: Module-2 |
Grade: test-sat Lesson: S2-T2 |
Explanation: Hello Students, time to practice and review. Let us take next 10-15 minutes to solve the ten problems using the Quiz Sheet. Then submit the quiz to get the score. This is a good exercise to check your understanding of the concepts. |
Quiz: in Class
| Problem Id | Problem | Options |
|---|---|---|
1 |
There are 55 students in the Spanish club. A sample of the Spanish club students was selected at random and asked whether they intend to enroll in a new study program. Of those surveyed, 20% responded that they intend to enroll in the study program. Based on this survey, which of the following is the best estimate of the total number of Spanish club students who intend to enroll in the study program? |
A) 55 B) 20 C) 44 D) 11 |
2 |
Jay walks at a speed of 3 miles per hour and runs at a speed of 5 miles er hour. He walks for w hours and runs for r hours for a combined total of 14 miles. Which equations represents this situation? |
A) 2w + 5r = 14 B) 3w + 14r = 14 C) 3w + 5r = 14 D) 3w - 5r = 28 |
3 |
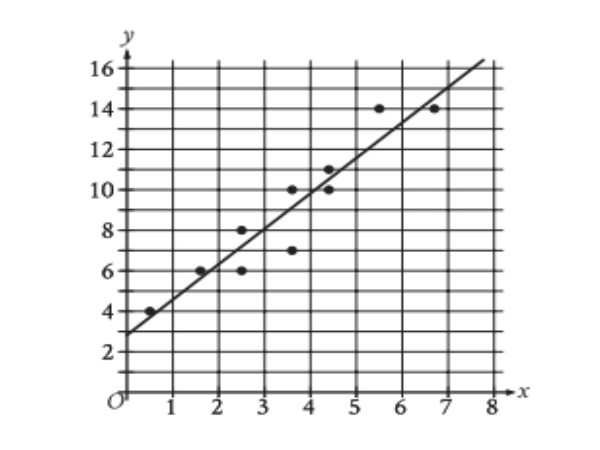
The scatterplot shows the relationship between two variables, x and y. A line fit is also shown.
Which of the following equations best represents the line of best fit shown? |
A) \$y = 2.8 + 1.7x\$ B) \$y = 2.8 - 1.7x\$ C) \$y = -2.8 + 1.7x\$ D) \$y = -2.8 - 1.7x\$ |
4 |
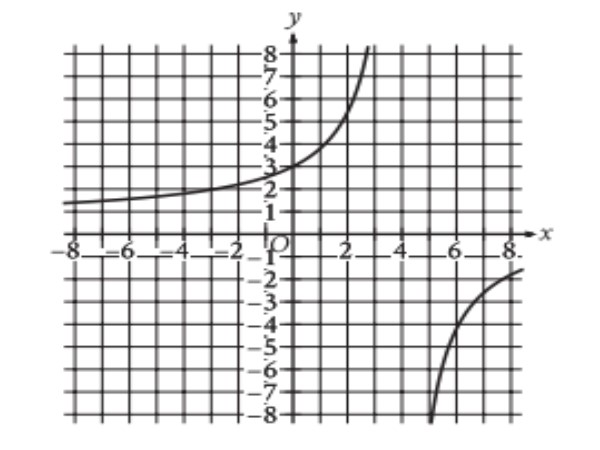
The graph of y = f(x) is shown in the xy plane. What is the value of f(0)?
|
A) -3 B) 0 C) 3 D) \$3/5\$ |
5 |
Which expression is equivalent to \$(m^4q^4z^-1),(mp^5z^3)\$ where m, q, and z are positive? |
A) \$m^5q^9z^2\$ B) \$m^4q^20z^-3\$ C) \$m^6q^8z^-1\$ D) \$m^20q^12z^-2\$ |
6 |
73, 74, 75, 77, 79, 82, 84, 85, 91 What is the median of the data shown? |
A) 20 B) 65 C) 79 D) 50 |
7 |
\$x + 40 = 95\$ |
A) 55 B) 58 C) 30 D) 75 |
8 |
\$5x = 15\$ |
A) −17 B) −13 C) 17 D) 13 |
9 |
\$g(m) = -0.5m + 12.1\$ |
A) 20 B) 12.1 C) 0.05 D) 242.0 |
10 |
\$1/(7b) = (11x)/y\$ |
A) \$x = (7by)/11\$ B) \$x = y - 77b\$ C) \$x = y/(77b)\$ D) \$77by\$ |
11 |
\$y = 76\$ |
A) \$-76/5\$ B) 5 C) - 9 D) 76 |
12 |
\$y > 14\$ |
A) −9 B) −5 C) 5 D) 9 |
13 |
Out of 300 seeds that were planted, 80% sprouted. How many of these seeds sprouted? |
A) 183 B) 218 C) 240 D) 160 |
14 |
The function f is defined by \$f(x) = 4x\$. For what value of x does \$f(x) = 8\$? |
A) 5 B) 4 C) 1 D) 2 |
15 |
Which expression is equivalent to \$(8x(x-7)-3(x-7))/(2x-14)\$, where \$x > 7\$? |
A) \$(x-7)/5\$ B) \$(8x^2-3x-14)/(2x-14)\$ C) \$(8x-3)/2\$ D) \$(8x^2-3x-77)/2x-14\$ |
16 |
Line p is defined by \$2y + 18x = 9\$. Line Line r is perpendicular to line p in the xy-plane. What is the slope of line r ? |
A) −9 B) \$-1/9\$ C) 9 D) \$1/9\$ |
17 |
\$f(t) = 8,000(0.65)^t\$ |
A) The minimum estimated number of coupons the company sent to their customers during the 5 years was 1,428. B) The minimum estimated number of coupons the company sent to their customers during the 5 years was 8,000. C) The estimated number of coupons the company sent to their customers at the end of 1998 was 8,000. D) The estimated number of coupons the company sent to their customers at the end of 1998 was 1,428. |
18 |
Traingle XYZ is similar to triangle RST such that X,Y, and Z correspond to R, S, and T, respectively. The measure of \$\angleZ\$ is \$20^(\circ)\$ and 2XY = RS. What is the measure of \$\angleT\$? |
A) 20 degrees B) 10 degrees C) 2 degrees D) 40 degrees |
19 |
\$y = 6x + 18\$ |
A) \$-6 + y = 18\$ B) \$12x + y = 18\$ C) \$-12x + y = 36\$ D) \$-6x + y = 22\$ |
20 |
What is the area, in square centimeters, of a rectangle with a length of 34 centimeters (cm) and a width of 29 cm? |
A) 520 B) 986 C) 732 D) 325 |
21 |
\$y = 4x + 1\$ |
A) 35 B) 20 C) 36 D) 32 |
22 |
\$5x^2 + 10x + 16 = 0\$ |
A) Exactly one B) Exactly two C) Zero D) Infinitely many |
23 |
A certain park has an area of 11,863,808 square yards. What is the area, in square miles, of this park? (1 mile = 1,760 yards) |
A) 3.83 B) 1.96 C) 3,444.39 D) 6,740.8 |
24 |
Which of the following equations represents a circle in the xy-plane that intersects the y-axis at exactly one point? |
A) \$(x-8)^2+(y-8)^2=16\$ B) \$(x-8)^2+(y-4)^2=16\$ C) \$(x^2+(y-9)^2=16)\$ D) \$(x-4)^2+(y-9)^2=16\$ |
25 |
In triangles ABC and DEF, angles B and E each have measure 27degrees and angles C and F each have measure 41degrees. Which additional piece of information is sufficient to determine whether triangle ABC is congruent to triangle DEF? |
A) The measure of angle A B) The length of side AB C) The lengths of sides BC and EF D) No additional information is necessary. |
26 |
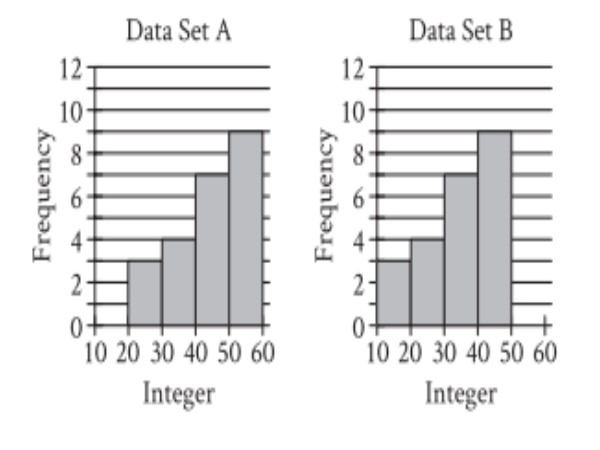
Two data sets of 23 integers each are summarized in the histograms shown. For each of the histograms, the first interval represents the frequency of integers greater than or equal to 10, but less than 20. The second interval represents the frequency of integers greater than or equal to 20, but less than 30, and so on. What is the smallest possible difference between the mean of data set A and the mean of data set B?
|
A) 0 B) 10 C) 1 D) 23 |
27 |
A right triangle has legs with lengths of 24 centimeters and 21 centimeters. If the length of this triangle’s hypotenuse, in centimeters, can be written in the form \$3\sqrtd\$, where d is an integer, what is the value of d? |
A) 178 B) 113 C) 110 D) 195 |
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 06-August-2024 09:20AM EST