SaiBook.us SAT-3

Lesson Example Discussion Quiz: Class Homework

Lesson

Title: Geometry

Grade: Core-SAT3 Lesson: S3-P1

Explanation: Hello students, let us learn a new topic in SAT-3 today with definitions, concepts, examples, and worksheets included.

Lesson:

Definition: Circle

A circle is a geometric shape consisting of all points in a plane that are at a constant distance, known as the radius, from a fixed point, called the center.

The total distance around the circle, calculated as C = \$2πr\$

The total region enclosed by the circle, given by A = \$πr^2\$

$1$

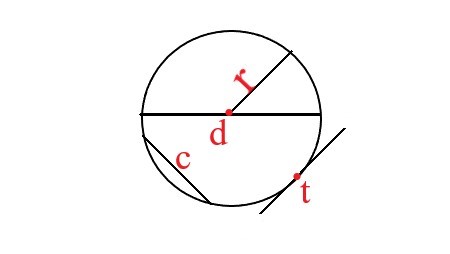
Explanation: In this image, the parts of a circle are radius(r), diameter(d), chord(c), tangent(t).

Definition: Triangle

A triangle is a polygon with three edges and three vertices. The three vertices are connected by line segments called sides, and the angles between these sides are called the interior angles. The sum of the interior angles of a triangle is always 180 degrees.
The area of a triangle can be calculated using various formulas, depending on the given information. The most common formula is:
A = \$1/2 bh\$, where b is base and h is height.
The perimeter of a triangle is the total length of its three sides. For a triangle with side lengths a, b, and c, the perimeter P is: \$P = a + b + c\$.

$2$

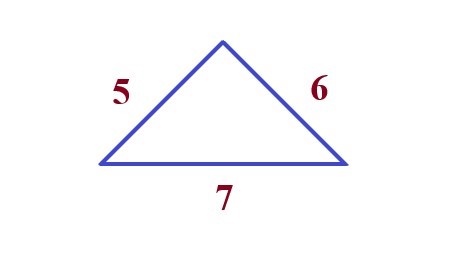
Explanation: In this example, we need to find out the area of the triangle using given three sides 5 , 6 , 7 units in length \$\sqrt(s(s-a)(s-b)(s-c))\$ then we get \$6 \sqrt6\$ square units.

Definition: Slope of a Line

The slope of a line can be calculated using two points lying on a straight line. Given the coordinates of the two points, we can apply the slope of the line formula. Let the coordinates of those two points be, P1 = (x1, y1) P2 = (x2, y2).

$3$

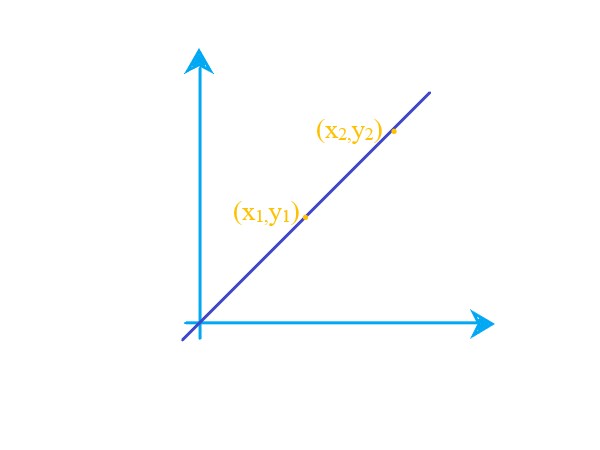
Explanation: To find the slope of a line, use an equation, m = \$(y2 - y1)/(x2 - x1)\$ where m is the slope of the line.

Definition: Line Segment

A line segment has two definite endpoints in a line. The length of the line segment is fixed, which is the distance between two fixed points.

The length here can be measured by metric units such as centimeters (cm), millimeters (mm), or conventional units like feet or inches.

A line segment is usually represented by the bar symbol (—) on top of the end points.

$4$

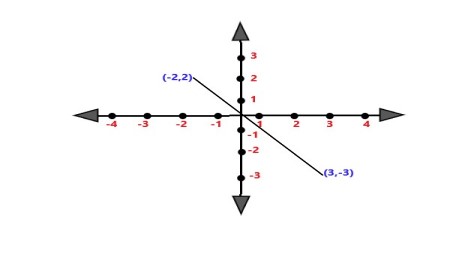
Explanation: The line segment between (-2, 2) and (3, -3) is about \$\sqrt (50)\$ units long using the distance formula.

Hint:\$\sqrt ((x2 - x1)^2 + (y2 - y1)^2)\$