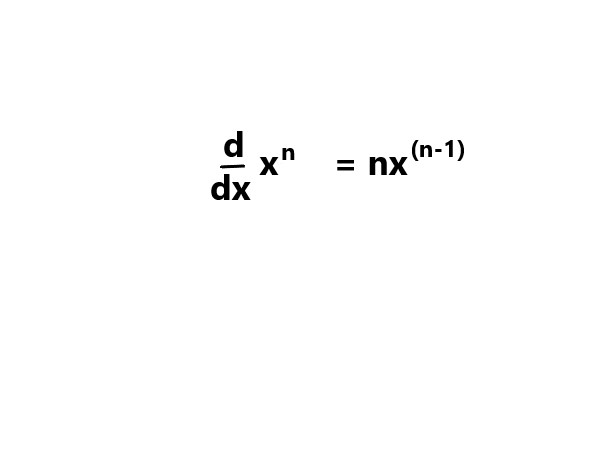
Explanation: Here, the given image shows the derivatives of elementary functions are remembered as differentiation formulas.

Integration is a mathematical process that finds the area under a curve or the accumulation of quantities. It can also be used to find the original function from its rate of change (its derivative).

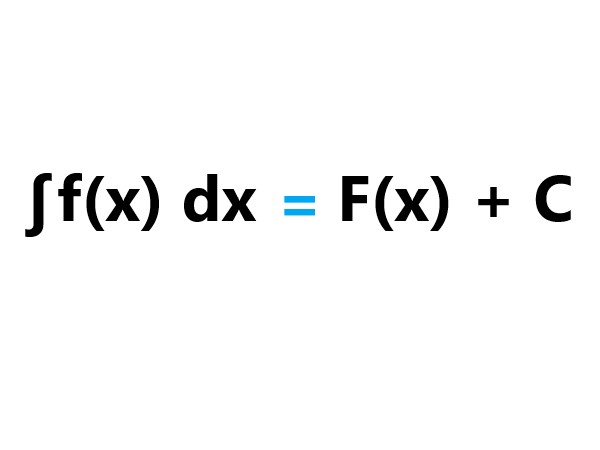
Explanation: The notation \$ ∫f(x)dx \$ denotes the integration of a function, where f(x) is the integrand and dx is the variable of integration. The antiderivative or indefinite integral of f(x) is represented by F(x), which is unique to an additive constant C.

An infinite sequence is a never-ending list of elements, where each element is associated with a positive integer index and there is no last element in the sequence.

Mathematically, an infinite sequence can be represented as:

\$ a = (a_1, a_2, a_3, ...) . \$

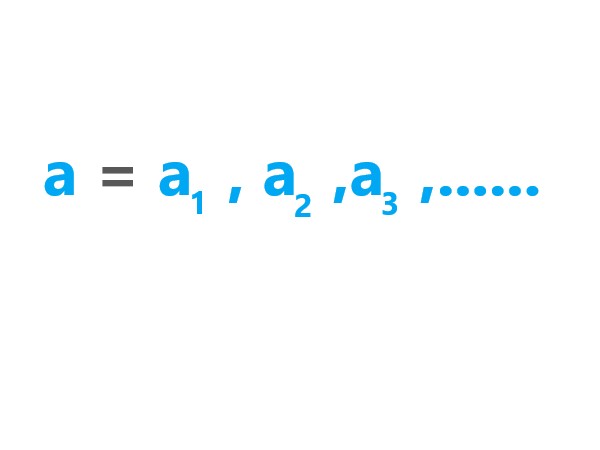
Explanation: Here, 'a' is the name of the sequence, and \$ a_1, a_2, a_3, ... \$ are the individual elements of the sequence.

An infinite series is a mathematical representation of the sum of an infinite sequence of numbers. It is denoted by the following general form:

\$ S = a_1 + a_2 + a_3 + a_4 + ... \$ .

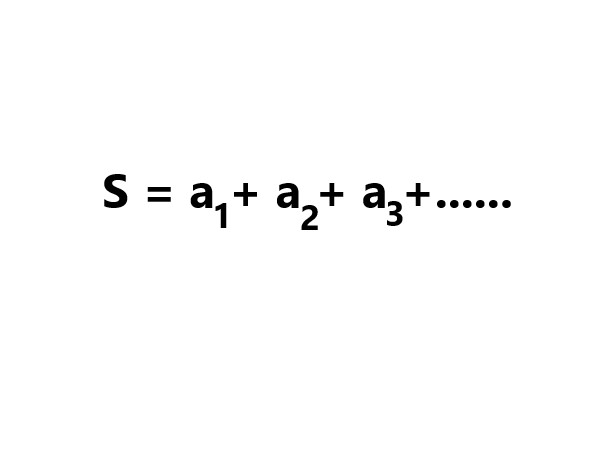
Explanation: Here, 'S' represents the sum of the infinite series, and '\$ a_1, a_2, a_3, ... \$' are the individual terms of the sequence.

Complex numbers are a mathematical extension of real numbers which introduce the imaginary unit denoted by "i". The imaginary unit is defined as the square root of -1, represented as \$i^2 = -1\$. A complex number is written in the format of
"a + bi".

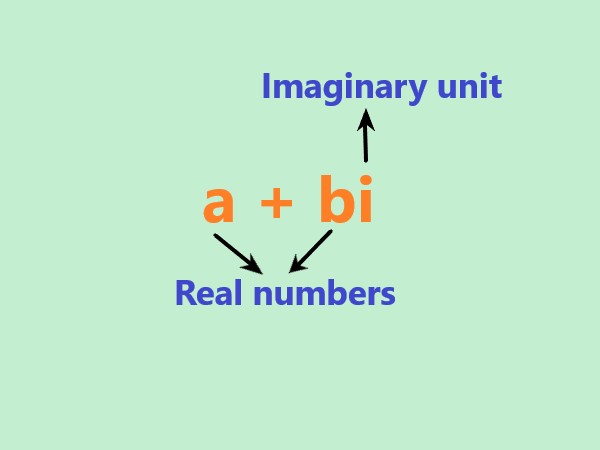
Explanation: The given image shows "a" is the real part, representing the horizontal component. "bi" is the imaginary part, representing the vertical component multiplied by the imaginary unit "i".