SaiBook.us SAT-3

Lesson Example Discussion Quiz: Class Homework

Lesson

Title: Algebra

Grade: Best-SAT3 Lesson: S5-P2

Explanation: Hello students, let us learn a new topic in SAT-3 today with definitions, concepts, examples, and worksheets included.

Lesson:

Definition: Equivalent Expressions

Equivalent expressions are mathematical expressions that represent the same value or produce the same result, even if they look different or use different operations or variables. They can be transformed into each other through algebraic manipulations like simplifying, factoring, expanding, or rearranging.

$1$

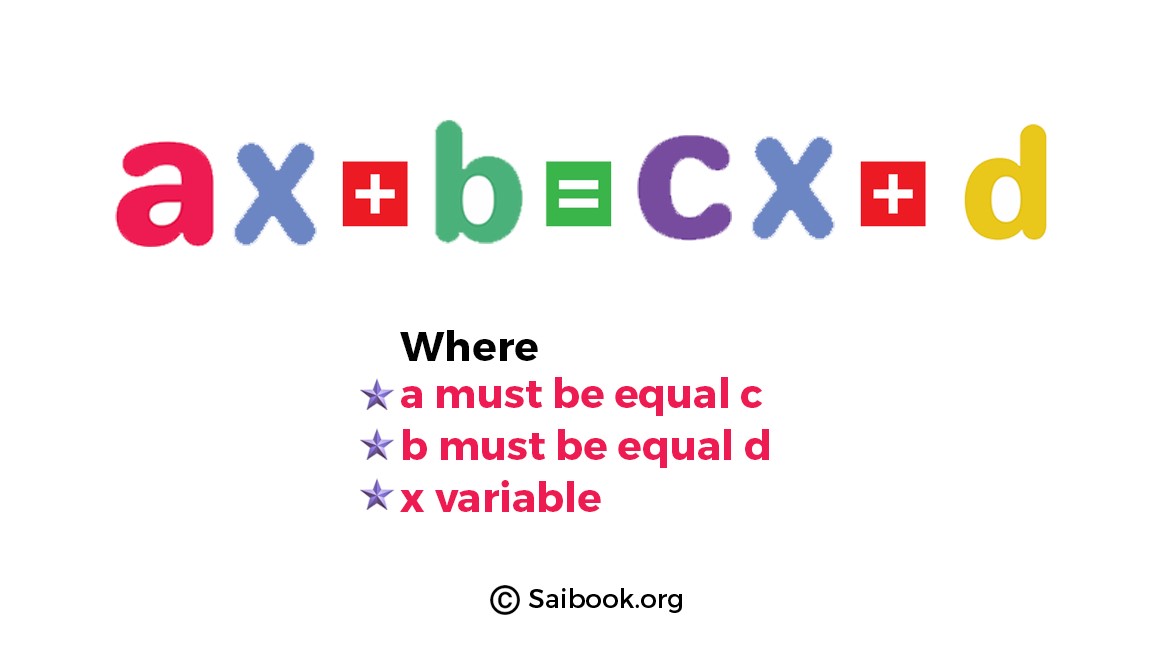
Explanation: Here, the given image shows it’s evident that a equals c and b equals d, while x varies as a variable.

Definition: Non-linear Equations

A nonlinear equation is an equation that doesn’t form a straight line when graphed. Nonlinear systems involve terms beyond linear or constant, like quadratic, cubic, exponential, and logarithmic functions. They’re described by equations where variables appear in polynomials of degree higher than one or in non-polynomial function arguments.

The general representation of nonlinear equations is;

\$ax^2 + by^2 =c\$

$2$

Explanation: The image displays a non-linear equation using x and y as variables, and a, b, and c as constants.

Definition: System of Linear Equations with Infinite Solutions

To solve systems of an equation in two or three variables, first, we need to determine whetherthe equation is dependent, independent, consistent, or inconsistent.

If a pair of linear equations have unique or infinite solutions, then the system of equations is said to be a consistent pair of linear equations.

Thus, suppose we have two equations in two variables as follows:

\$a_1 x + b_1y = c_1\$ equation(1)
\$a_2 x + b_2 y = c_2\$ equation(2)

$3$

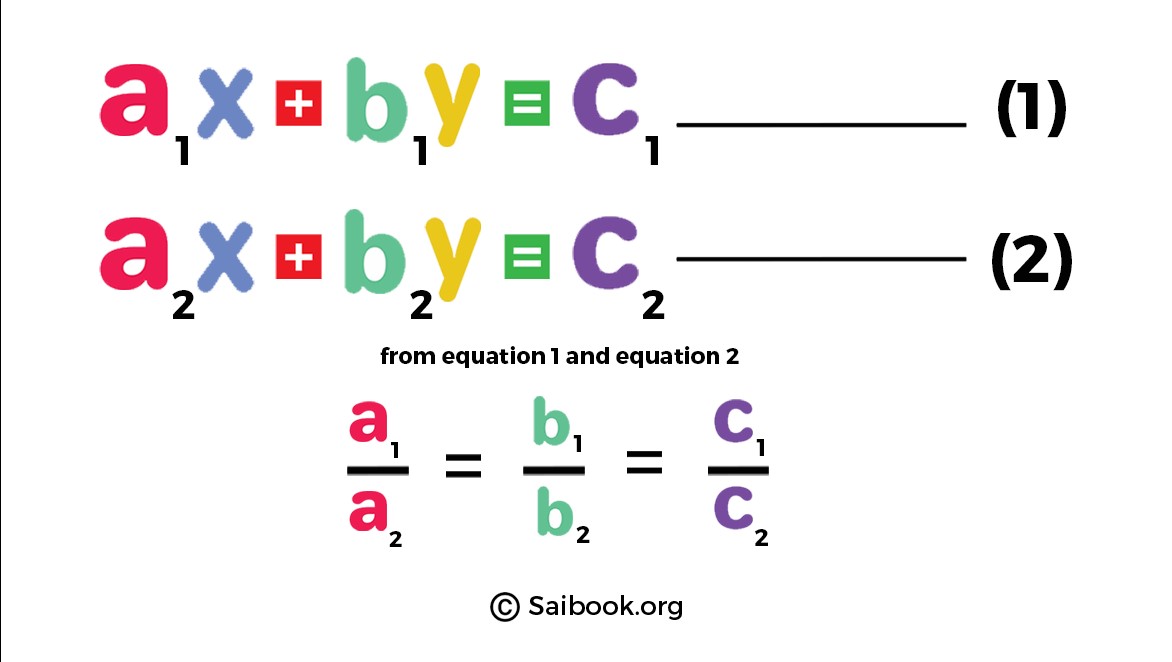
Explanation: Here the given image show that
\$a_1 x + b_1y = c_1\$ equation(1)
\$a_2 x + b_2 y = c_2\$ equation(2)

The given equations are consistent and dependent, and have infinitely many solutions if and only if,

\$(a_1/a_2) = (b_1/b_2) = (c_1/c_2)\$

Definition: System of Linear Equations with no Solutions

A system of linear equations with no solutions means that there are no values for the variables that can satisfy all the equations in the system simultaneously.

In other words, the equations are contradictory and cannot be accurate at the same time.

$4$

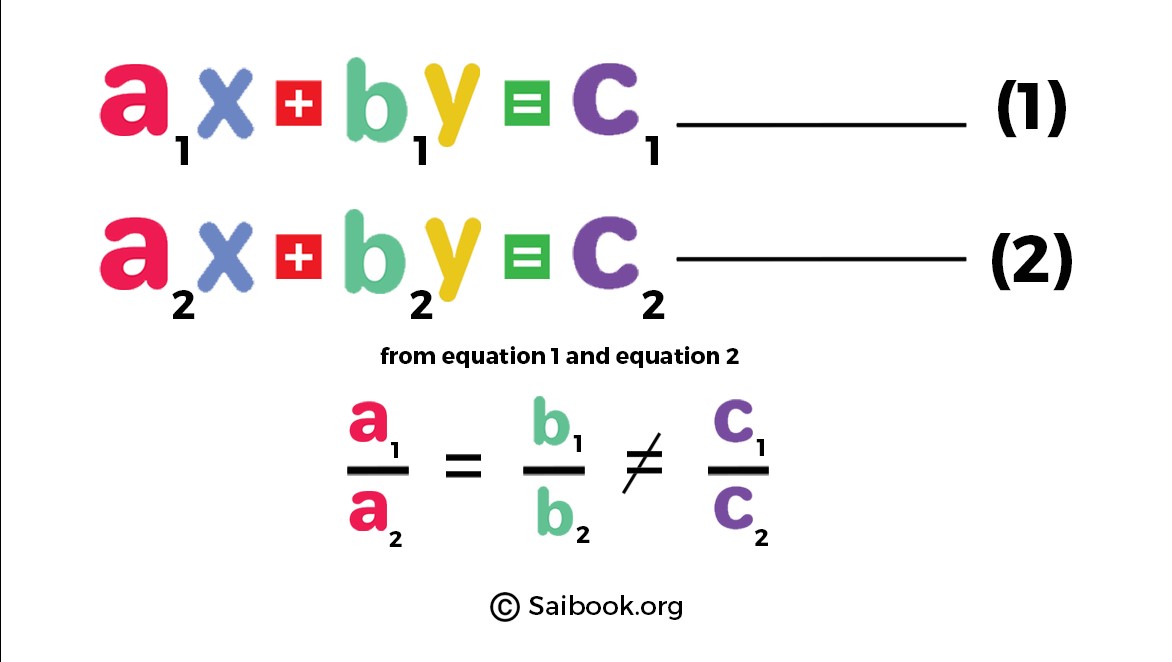
Explanation: Here, the given images shows,

\$a_1 x + b_1y = c_1\$ equation(1)

\$a_2 x + b_2 y = c_2\$ equation(2)

The system of equations is inconsistent and possesses no solutions only when,

\$(a_1/a_2) = (b_1/b_2) ne (c_1/c_2)\$