SaiBook.us SAT-3

Lesson Example Discussion Quiz: Class Homework

Lesson

Title: Geometry

Grade: Best-SAT3 Lesson: S3-P1

Explanation: Hello students, let us learn a new topic in SAT-3 today with definitions, concepts, examples, and worksheets included.

Lesson:

Definition: Circle

A circle is a closed curve in which all points are equally distant from a fixed point called the center. The fixed distance from the center to any point on the circle is called the radius.
The standard equation of a circle in the Cartesian coordinate system with center (h, k) and radius r is given by: \$("x" - "h")^2 + ("y" - "k")^2 = "r"^2\$, where (h, k) are the coordinates of the center of the circle.

$1$

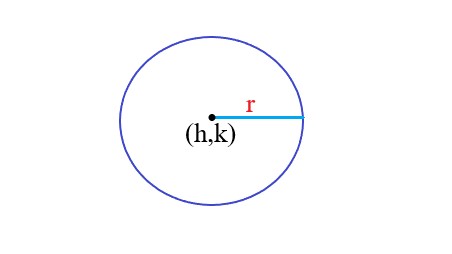
Explanation: In this image, h and k represent the center of the circle and r represents the radius.

Definition: Area of Sector

A sector of a circle is a portion of the circle enclosed by two radii and an arc between them. The area of a sector can be calculated using the formula: Area of Sector = \$("central Angle"/(360°)) \times π"r"^2\$, where Central Angle is the angle formed by the radii at the center of the circle (measured in degrees), and r is the radius of the circle.

$2$

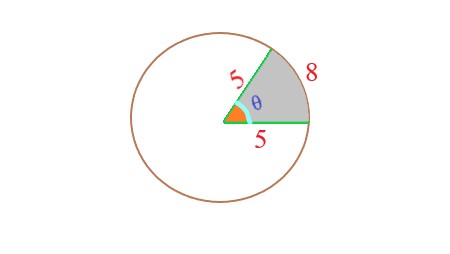
Explanation: In this image, the radius of 5 units and an arc length of 8 units, the sector of the circle defined by this arc length has an area of 20 square units, as determined by the formula \$"A" = ("s" \times "r")/2\$

Definition: Triangle

A triangle is a polygon with three edges and three vertices. The three vertices are connected by line segments called sides, and the angles between these sides are called the interior angles. The sum of the interior angles of a triangle is always 180 degrees.
The area of a triangle can be calculated using various formulas, depending on the given information. The most common formula is:
A = \$1/2 bh\$, where b is base and h is height.
The perimeter of a triangle is the total length of its three sides. For a triangle with side lengths a, b, and c, the perimeter P is: \$P = a + b + c\$.

$3$

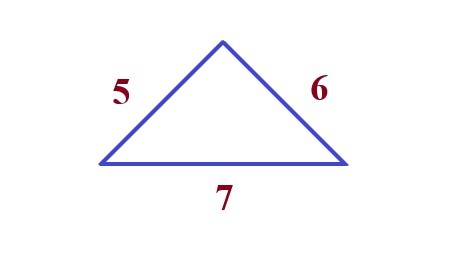
Explanation: In this example, we need to find out the area of the triangle using given three sides 5 , 6 , 7 units in length \$\sqrt(s(s-a)(s-b)(s-c))\$ then we get \$6 \sqrt6\$ square units.

Definition: Slope of Line

The slope of a line can be calculated using two points lying on a straight line.
The two points (x1, y1) and (x2, y2) on the line segment, the slope m is calculated as:
m = \$(y2 - y1)/(x2 - x1)\$
The slope is positive, the line segment rises as it moves from left to right.
The slope is negative, the line segment falls as it moves from left to right.
The slope is zero, the line segment is horizontal.

$4$

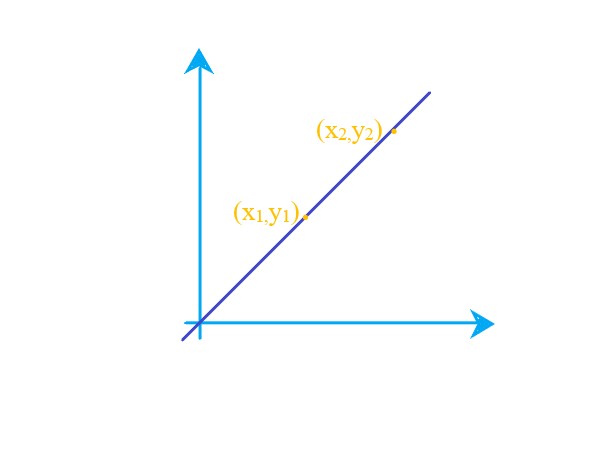
Explanation: To find the slope of a line, use an equation, m = \$(y2 - y1)/(x2 - x1)\$ where m is the slope of the line.