Lesson Example Discussion Quiz: Class Homework |
Quiz In Class |
Title: Calculus |
Grade: Top-SAT3 Lesson: S6-P1 |
Explanation: Hello Students, time to practice and review. Let us take next 10-15 minutes to solve the ten problems using the Quiz Sheet. Then submit the quiz to get the score. This is a good exercise to check your understanding of the concepts. |
Quiz: in Class
| Problem Id | Problem | Options |
|---|---|---|
1 |
Solve the equation |
A) x = 4 and x = - 3 B) x = 3 and x = 2 C) x = - 5 and x = 4 D) x = 3 and x = - 2 |
2 |
The equation \$e^4x + 8e^3x + 13e^2x - 8e^x + 1 = 0\$, x ∈ R has: |
A) Two solutions and only one of them is negative. B) Two solutions and both are negative. C) Four solutions two of which are negative. D) No solution. |
3 |
Find the limit \$lim_(x->∞) ((x^2 + x + 1) / (3x + 2)^2)\$. |
A) 0 B) \$1/9\$ C) 1 D) \$1/3\$ |
4 |
Let λ ≠ 0 be a real number. Let α, β be the roots of the equation \$14x^2 - 31x + 3λ\$ = 0 and α, γ be the roots of the equation \$35x^2 - 53x + 4λ\$ = 0. Then \$(3α) / β\$ and \$(4α) / γ\$ are the roots of the equation. |
A) \$7x^2 - 245x + 250 = 0\$ B) \$49x^2 + 245x + 250 = 0\$ C) \$49x^2 - 245x + 250 = 0\$ D) \$7x^2 + 245x - 250 = 0\$ |
5 |
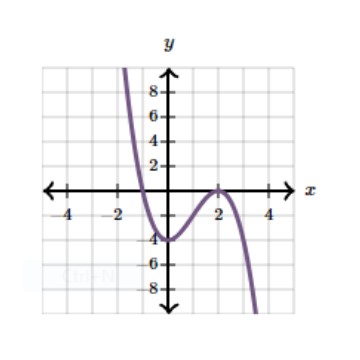
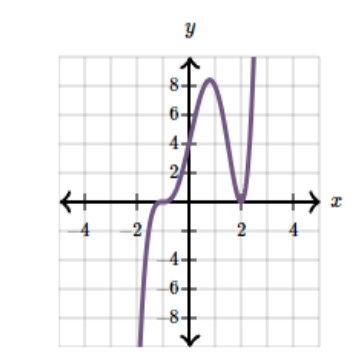
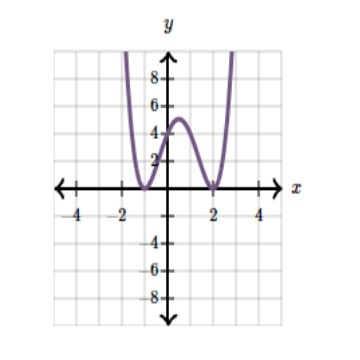
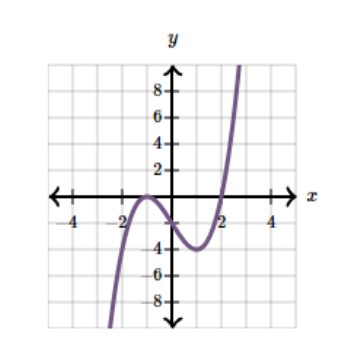
Which of the following could be the graph of \$y = k(x - 2 )^m (x + 1)^n\$, where k is a real number, m is an even integer, and n is an odd integer? |
A) B) C) D) |
6 |
Find the x-values for which \$"f(x)" = 2/(sqrt(1 - x))\$ continuous. |
A) (∞, 4) B) (− ∞, 3) C) (− ∞, 1) D) (∞, 2) |
7 |
Solve each of the inequalities \$x^6 - 4x^4 - 16x^2 + 64 ≥ 0\$. |
A) \$ x ∈ (- ∞, - 2) ∪ (2, ∞)\$ B) \$ x ∈ (- ∞, - 1) ∪ (1, ∞)\$ C) \$ x ∈ (- ∞, - 2) \$ D) \$ x ∈ (2, ∞)\$ |
8 |
If the quadratic equation \$x^2 + px + q = 0\$ has roots α and 𝛽, \$α^2 + β ^2 = 7\$ and α + β =3 , find the values of p and q. |
A) p = - 3 and q = - 1 B) p = 3 and q = 1 C) p = 3 and q = - 1 D) p = - 3 and q = 1 |
9 |
Rahul and Rohan have 45 marbles together. After losing 5 marbles each, the product of the number of marbles they both have now is 124. How to find out how many marbles they had to start with. |
A) x = - 36, x = - 9 B) x = 36, x = 9 C) x = 36, x = - 9 D) x = - 36, x = 9 |
10 |
Find the horizontal and vertical asymptotes of \$ f(x)= (3x^2-9x)/ (x^2-9) \$. |
A) Horizontal Asymptote: y = 3 B) Horizontal Asymptote: y = 3 C) Horizontal Asymptote: y = 3 D) Horizontal Asymptote: y = 4 |
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 17-July-2024 09:20AM EST