Lesson Example Discussion Quiz: Class Homework |
Quiz In Class |
Title: Linear inequalities in one or two variables |
Grade: 1400-a Lesson: S1-L4 |
Explanation: Hello Students, time to practice and review. Let us take next 10-15 minutes to solve the ten problems using the Quiz Sheet. Then submit the quiz to get the score. This is a good exercise to check your understanding of the concepts. |
Quiz: in Class
| Problem Id | Problem | Options |
|---|---|---|
1 |
y ≤ x + 7 and y ≥ - 2x - 1 |
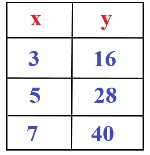
A) (-14, 0) B) (0, 14) C) (14, 0) D) (0, -14) |
2 |
A small business owner budgets $2,200 to purchase candles. The owner must buy at least 200 candles to maintain the discounted pricing. Suppose the owner pays $4.90 per candle to purchase small candles and $11.60 per candle to purchase large candles. What is the maximum number of large candles the owner can buy to stay within the budget and maintain the discounted pricing? |
A) 125 B) 128 C) 152 D) 182 |
3 |
If \$a + b = 2m^2\$, b + c = 6m, a + c = 2, where m is the real number and a ≤ b ≤ c, then which one of the following is correct? |
A) \$0 ≤ "m" ≤ 1/2\$ B) \$1/3 ≤ "m" ≤ 1\$ C) -1 ≤ m ≤ 0 D) None of the above |
4 |
y < 6x + 2 |
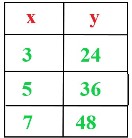
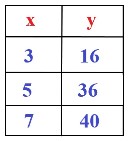
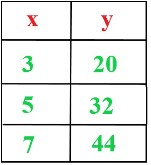
A) B) C) D) |
5 |
A classroom can fit at least 9 tables with an area of a one-meter square. We know that the perimeter of the classroom is 12m. Find the bounds on the length and breadth of the classroom. |
A) L < 3 and B > 3 B) L = 3 and B = 3 C) L > 3 and B < 3 D) 0 |
6 |
Solve the compound inequality: |
A) \$ (−2, 5/4) \$ B) \$ (−1, 5/4) \$ C) \$ (−1, 5/7) \$ D) \$ (−3, 5/2) \$ |
7 |
A company needs to produce at least 100 units of product A and at least 150 units of product B. Product A requires 2 hours of labor per unit, and product B requires 3 hours per unit. The company has a total of 900 hours of labor available. Write down a system of inequalities to represent this situation. |
A) \$ "x" ≤ 100, "y" ≥ 150, 2"x" + 3"y" ≤ 900 \$ B) \$ "x" ≥ 100, "y" ≥ 150, 2"x" + 3"y" ≤ 900 \$ C) \$ "x" ≥ 100, "y" ≤ 150, 2"x" + 3"y" ≤ 900 \$ D) \$ "x" ≤ 100, "y" ≥ 150, 2"x" + 3"y" ≥ 900 \$ |
8 |
Solve the compound inequality and express the solution in interval notation: |
A) \$ (−∞, −1) ∪ (−∞, 2)\$ B) \$ (−∞, −2) ∪ (−∞, 4)\$ C) \$ (−∞, −1) ∪ (−∞, 4)\$ D) \$ (−∞, 1) ∪ (−∞, 5)\$ |
9 |
A landscaper is designing a rectangular garden. The length of the garden must be at least 3 meters longer than its width. If the perimeter of the garden is less than or equal to 80 meters, write and solve a system of inequalities to represent the possible dimensions of the garden. |
A) \$"l" = "w" + 1, "w" ≤ 18.5, "w" ≥ 1 \$ B) \$"l" = "w" + 3, "w" ≤ 12.5, "w" ≥ 0 \$ C) \$"l" = "w" + 3, "w" ≤ 18.5, "w" ≥ 0 \$ D) \$"l" = "w" + 2, "w" ≤ 18.5, "w" ≥ 0 \$ |
10 |
Find the set of all points (x, y) that satisfy the inequality: |
A) \$ \∣ (x, y) \∣ "x" ≤ 1\$ and \$"y" ≤ 1 \$ B) \$ \∣ ("x", "y") \∣ "x" ≤ 1\$ and \$"y" ≤ 0 \$ C) \$ \∣ ("x", "y") \∣ "x" ≤ 0\$ and \$"y" ≤ 1 \$ D) \$ \∣ ("x", "y") \∣ "x" ≤ 0\$ and \$"y" ≤ 0 \$ |
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 14-June-2024 09:20AM EST