Lesson Example Discussion Quiz: Class Homework |
Quiz In Class |
Title: Trigonometry ratios in right triangles |
Grade: 10-a Lesson: S3-L2 |
Explanation: Hello Students, time to practice and review. Let us take next 10-15 minutes to solve the ten problems using the Quiz Sheet. Then submit the quiz to get the score. This is a good exercise to check your understanding of the concepts. |
Quiz: in Class
| Problem Id | Problem | Options |
|---|---|---|
1 |
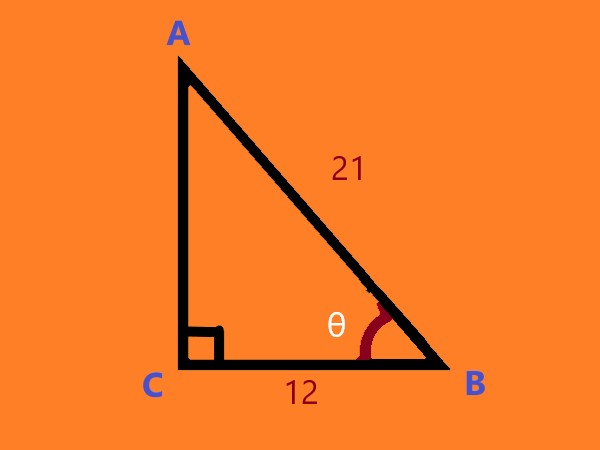
Consider △ACB, right-angled at C, in which AB = 21 units, BC = 12 units, and ∠ABC = \$ \theta \$ (see fig). Determine the values of \$ sin^2 \theta - cos^2 \theta \$.
|
A) \$ 53/147 \$ B) \$ 51/147 \$ C) \$ 23/162 \$ D) \$ 42/137 \$ |
2 |
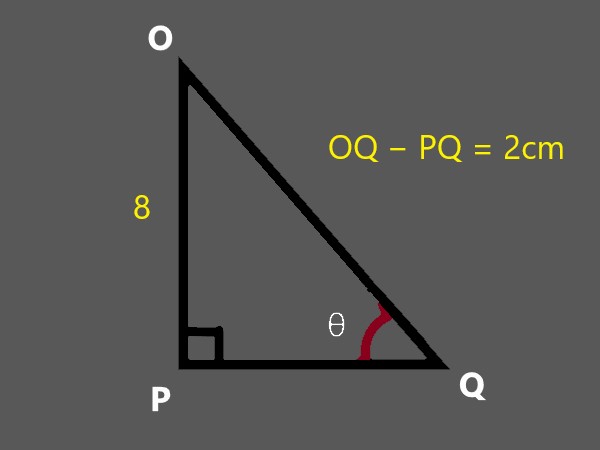
In △OPQ, right-angled at P, OP = 8cm, and OQ − PQ = 2cm, and determine the values of sinQ and cosQ.
|
A) \$ 8/11, 15/11\$ B) \$ 8/17, 15/17\$ C) \$ 11/17, 8/17\$ D) \$ 15/13, 8/13\$ |
3 |
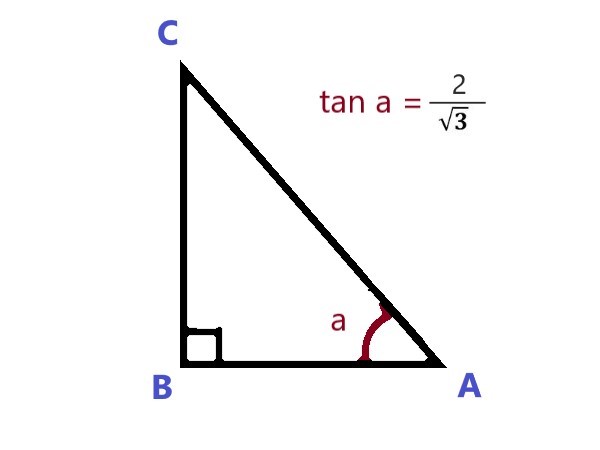
In ∆ ABC, right angled at B, if tan A = \$2/\sqrt3 \$ then the value of sin A + cos A is
|
A) \$ ( 1 + \sqrt3)/(\sqrt 7)\$ B) \$ ( 3 + \sqrt7)/(\sqrt 2)\$ C) \$ ( 3 + \sqrt2)/(\sqrt 7)\$ D) \$ ( 2 + \sqrt3)/(\sqrt 7)\$ |
4 |
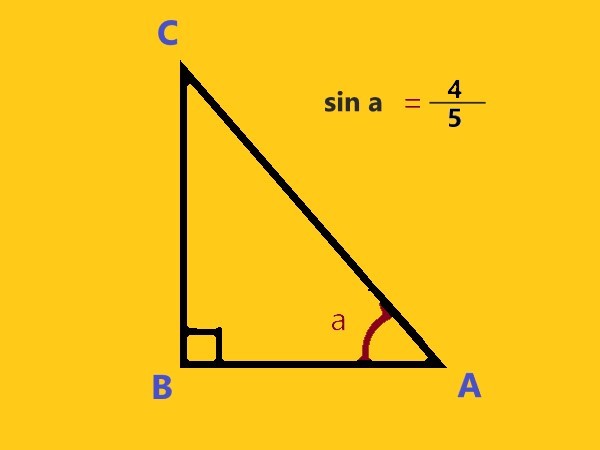
Given \$sinA = 4/5 \$, find the other trigonometric ratios of the angle A.
|
A) \$tan A = 4/3, cosA = 3/4, cscA = 5/4, secA = 4/3, cotA = 3/4 \$ B) \$tanA = - 4/3, cosA = - 3/5, cscA = 4/5, secA = 5/3, cotA = - 3/4 \$ C) \$tanA = 5/4, cosA = 5/3, cscA= 4/5, secA = 5/3, cotA= 4/3 \$ D) \$tanA = 4/3, cosA = 3/5, cscA = 5/4, secA = 5/3, cotA = 3/4 \$ |
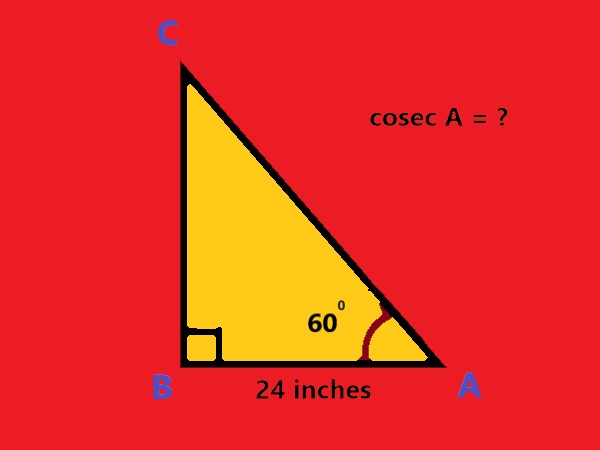
5 |
In a triangle ABC, right-angled at B, AB = 24 inches, and angle \$ A = 60^o\$. Find csc A.
|
A) \$ (\sqrt3)/2 \$ inches B) \$ (\sqrt2)/3 \$ inches C) \$ (2\sqrt3)/3 \$ inches D) \$ 1/(\sqrt3) \$ inches |
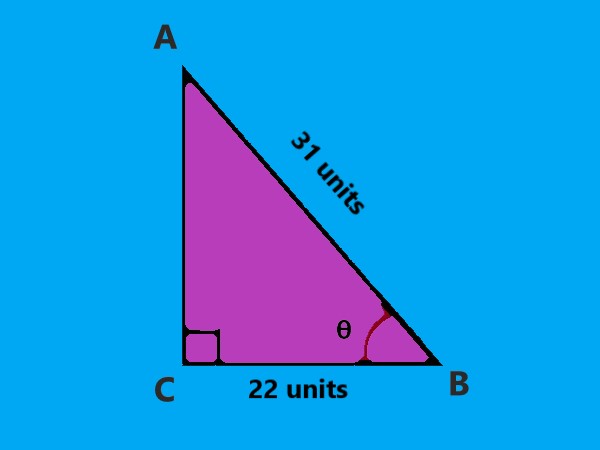
6 |
Consider △ACB, right angled at C, in which AC = 20 units, BC=21 units ∠ABC = \$ \theta \$. Determine the value of \$cos^2 \theta + sin^2 \theta\$ and \$cos^2 \theta - sin^2 \theta\$.
|
A) 0 and \$41/841\$ B) 1 and \$29/20\$ C) 1 and \$41/841\$ D) 0 and \$841/29\$ |
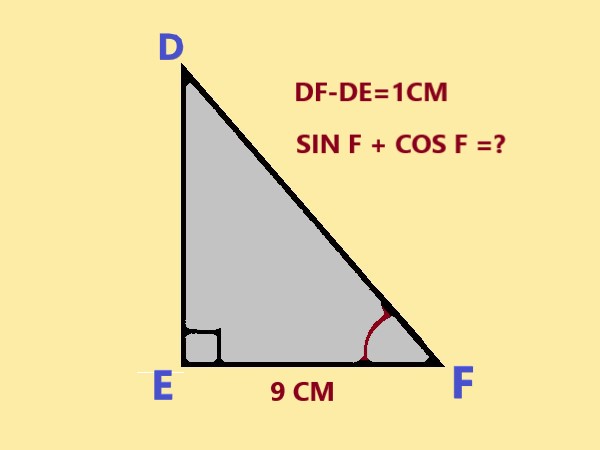
7 |
In △DEF, right-angled at E, EF = 9cm, and DF-DE = 1cm, and determine the values of sin F + cos F.
|
A) \$49/41\$ B) \$41/49\$ C) \$40/49\$ D) \$41/47\$ |
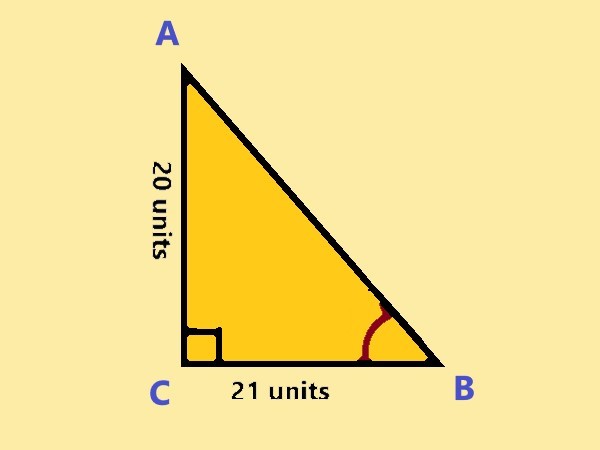
8 |
Consider △ACB, right-angled at C, in which AB = 31 units, BC = 22 units, and ∠ABC = \$ \theta \$ (see fig). Determine the values of \$ sin^2 \theta - cos^2 \theta \$.
|
A) \$7/961\$ B) \$961/7\$ C) \$41/49\$ D) \$49/41\$ |
9 |
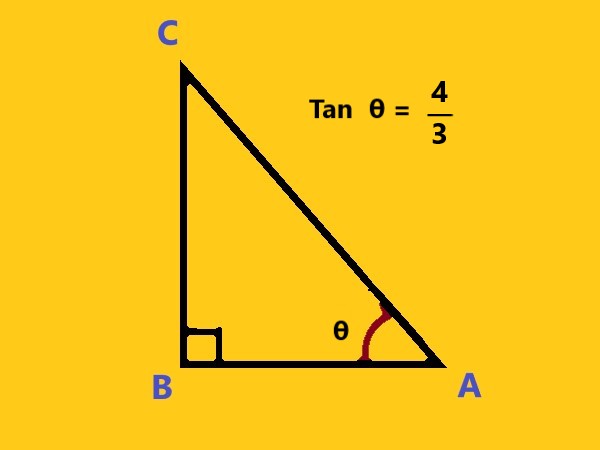
Given \$Tan \theta = 4/3 \$, find the other trigonometric ratios of the angle \$\theta\$.
|
A) \$sin \theta = 4/5, cos \theta = 3/4, csc \theta = 5/3, sec \theta = 4/3, cot \theta = 3/4 \$ B) \$sin \theta = 4/5, cos \theta = 3/4, csc \theta = 5/4, sec \theta = 4/3, cot \theta = 3/4 \$ C) \$sin \theta = 4/5, cos \theta = 3/4, csc \theta = 5/3, sec \theta = 4/3, cot \theta = 5/3 \$ D) \$sin \theta = 4/5, cos \theta = 3/5, csc \theta = 5/3, sec \theta = 4/3, cot \theta = 5/3 \$ |
10 |
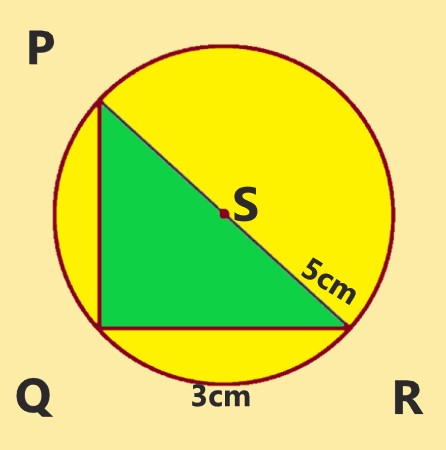
PQR is a triangle with Q as the right angle, PR = 5 cm, and RQ = 3cm. A circle is drawn with S as the center and SR as the radius. The length of the chord of this circle passing through P and Q is
|
A) 3 B) 4 C) 5 D) 6 |
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 07-June-2024 09:20AM EST