A quadratic equation is a polynomial equation of the second degree, meaning it has the highest exponent of 2. It is written in the general form:

\$"ax"^2 + "bx" + "c" = 0\$

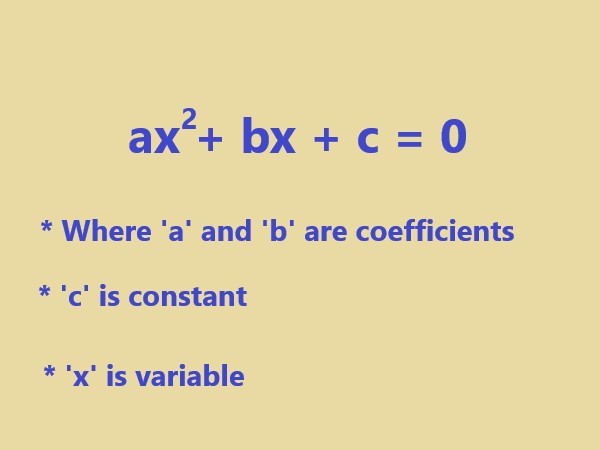
Explanation: Here the given image shows the where x represents the unknown variable, and a, b, are coefficients and c is constant.

The quadratic formula is a mathematical formula that can be used to find the solutions of any quadratic equation. The quadratic formula is given by:

\$ x = (-b ± \sqrt (b^2 - 4ac)) / (2a) \$

Explanation: In this formula, x represents the variable, while a, b, and c are coefficients (constants) of the quadratic equation \$"ax"^2 + "bx" + "c" = 0\$.

By substituting the values of a, b, and c into the quadratic formula, you can calculate the solutions for x. The
± symbol indicates that there are two possible solutions, one with a plus sign and the other with a minus sign.

Quadratic factors are the binomial expressions that result from breaking down a quadratic expression into its constituent parts through the process of factoring.

Explanation: Here, the provided image illustrates that a quadratic expression is an algebraic
expression of the form \$"ax"^2 + "bx" + "c"\$, where a, b, and c are constants, and x is the variable.