SaiBook.us SAT-1

Lesson Example Discussion Quiz: Class Homework

Example

Title: Subtraction Fractions

Grade: 8-a Lesson: S1-L6

Explanation: Hello Students, time to learn examples. Let us take turns and read each example. Explain each step. Pay special attention to steps and pictures and communicate in your own words.

Examples:

Subtract \$8 15/10 - 4 12/16\$.

Step 1a

First, convert the given mixed fractions into improper fractions.

⇒ Now multiply the denominator with a whole number and add the answer to the numerator.

⇒\$8 15/10\$ = \$95/10\$

⇒\$4 12/16\$ = \$76/16\$

$1a$

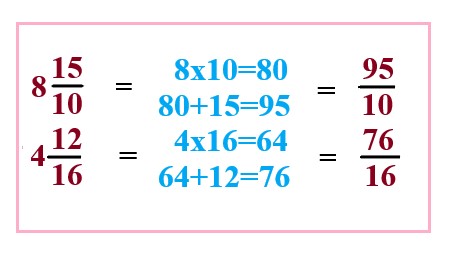
Explanation: Now multiply 8 by 10 and add 15 we get 95. Now multiply 4 by 16 and add 16 we get 76. we get

the fractions \$95/10-76/16 \$.

Step 1b

We add fractions with different denominators by finding the lowest common multiple of the denominators.

In this case, it’s 80 (the denominators are 10 and 16).

$1b$

Explanation: By performing LCM of 10 and 16 we get 80.

Step 1c

Multiply both the numerator and denominator of each fraction by the number that makes its denominator equal to the LCM.

\$((95\times8) - (76\times5))/80\$

$1c$

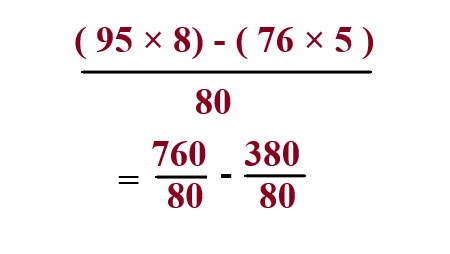
Explanation: Now multiply \$95/10\$ into \$8/8\$. Now multiply \$76/16\$ into \$5/5\$. we get
the fractions to \$760/80 -380/80 \$

Step 1d

The two fractions now have like denominators, so you can subtract the numerators.
\$(760 - 380)/80\$ = \$380/80\$

$1d$

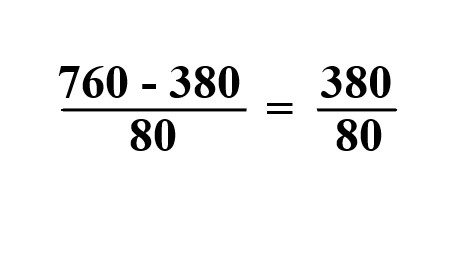
Explanation: Now subtract the numerator with common denominator 380 from 760 we get 380.

Step 1e

This fraction can be reduced by dividing both the numerator and denominator by using 20.

$1e$

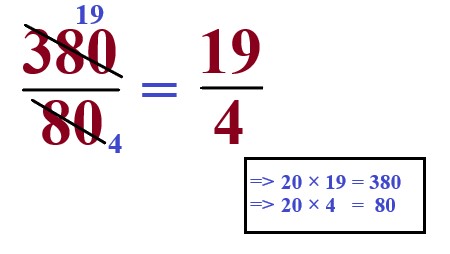
Explanation: 380 by 80 is divided by 20 we get \$19/4\$.

Step 1f

Divide the fraction \$19/4\$.

$1f$

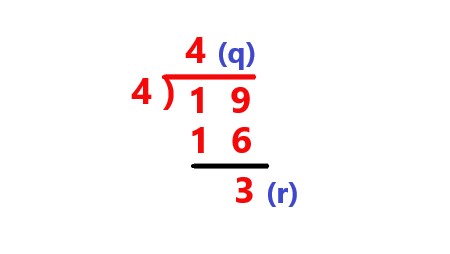
Explanation: By dividing 19 by 4 we get 4 as quotient and remainder as 3.

Step 1g

\$"Mixed fraction"\$ = \$"Whole number" + "Numerator" /"Denominator"\$

$1g$

Explanation: Therefore, the mixed fraction is \$4 3/4\$.