Lesson Example Discussion Quiz: Class Homework |
Quiz At Home |
Title: Area of 2D-shapes |
Grade: 1300-a Lesson: S3-L5 |
Explanation: Hello Students, time to practice and review. Let us take next 10-15 minutes to solve the ten problems using the Quiz Sheet. Then submit the quiz to get the score. This is a good exercise to check your understanding of the concepts. |
Quiz: at Home
| Problem Id | Problem | Options |
|---|---|---|
1 |
The area of a rectangle is 200. The ratio of the base to the height is 2:4. Find the base, the height, and the diagonal of the rectangle. |
A) b = 2 ,h = 20 B) b = 10 ,h = 20 C) b = 10 ,h = 12 D) b = 10 ,h = 20 |
2 |
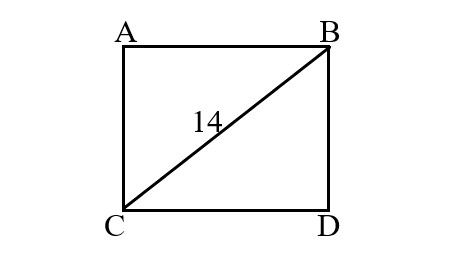
Find the area of square ABCD.
|
A)96 B) 99 C) 98 D) 89 |
3 |
A parallelogram has sides of lengths 8 units and 14 units, and one of its angles is 60 degrees. Find the area of the parallelogram. |
A) \$112\sqrt3\$ B) \$56\sqrt3/2\$ C) \$65\sqrt3\$ D) \$56\sqrt3\$ |
4 |
The length of a rectangle is twice its width. If the perimeter of the rectangle is 333 meters, what are the dimensions of the rectangle? What is its area? |
A) 6160.5 sq.units B) 6116.5 sq.units C) 5160.5 sq.units D) 6610.5 sq.units |
5 |
If the ratio of diagonals of two squares is 8: 12, then find the ratio of their corresponding areas. |
A) 2:3 B) 3:12 C) 8:3 D) 2:9 |
6 |
What is the positive difference in area between a parallelogram with a height of 12 and a base length of 15 and a triangle with a height of 8 and a base length of 10? |
A) 140 sq.units B) 120 sq.units C) 160 sq.units D) 140 units |
7 |
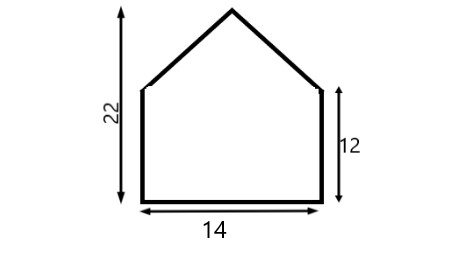
Find the area of the given irregular pentagone.
|
A)\$308 cm^2\$ B) \$308 cm\$ C) \$318 cm^2\$ D) \$388 cm^2\$ |
8 |
Find the area of the regular hexagon ABCDEF given that the area of one of the congruent triangles is \$10 cm^2\$. |
A) \$50\$ cm B) \$60 cm\$ C) \$40 cm\$ D) \$30 cm\$ |
9 |
Find the area of a regular pentagon whose side is 10 cm and apothem length is 8 cm. |
A) \$200 cm\$ B) \$100 cm^2\$ C) \$200 cm^2\$ D) \$400 cm^2\$ |
10 |
The area of a rhombus is 86 square units, and one of its diagonals is 12 units. Find the length of the other diagonal. |
A) 10.33 units B) 12.5 units C) 13 units D) 14.33 units |
Copyright © 2020-2022 saibook.us Contact: info@saibook.us Version: 1.5 Built: 10-June-2024 09:20AM EST