Definition: Quadratic-Equations

A quadratic equation is a second degree polynomial equation, meaning it has the highest exponent of 2. It is written in the general form:

\$ax^2 + bx + c = 0\$

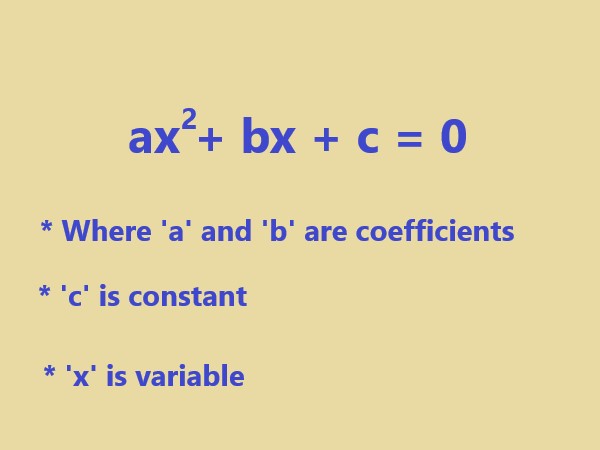
Explanation:

Here the given image shows the where x represents the unknown variable, and a, b, are coefficients and c is constant.

Definition: Polynomial Functions

Polynomial functions are mathematical functions that consist of variables raised to non-negative integer powers and multiplied by coefficients. They are expressed in the general form:

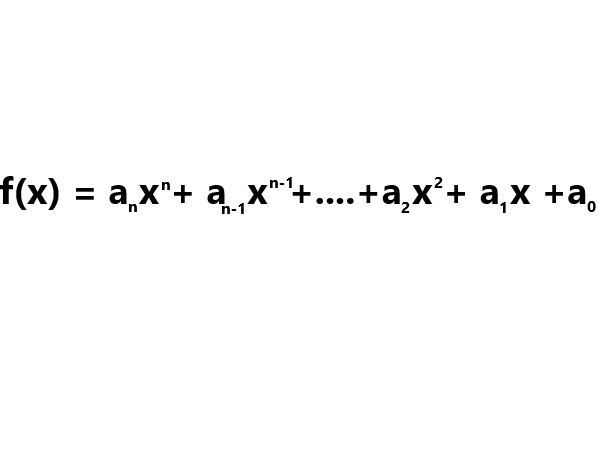
Explanation:

Here is an image that shows how f(x) represents a function, where x is a variable, and a₀, a₁, …​, aₙ are the coefficients. The degree of the polynomial is determined by the highest power of x in the function.

Definition: Rational Expression

A rational expression is an algebraic expression that represents a ratio or quotient of two polynomial expressions. It is essentially a fraction in which the numerator and denominator are polynomials.

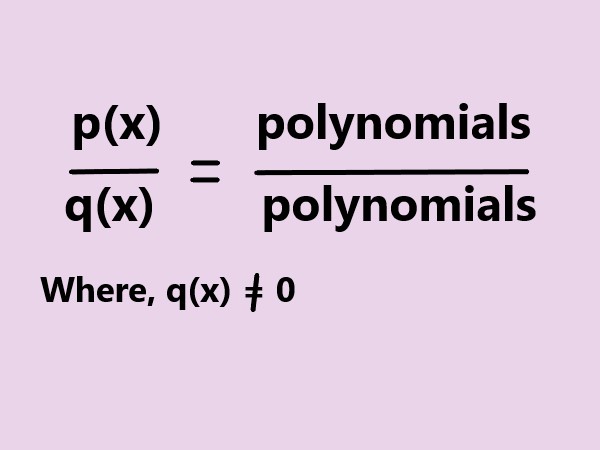
Explanation:

Here the given image shows the rational expression of the form \$(p(x))/(q(x)) = (polynomial)/(polynomial)\$

where q(x )≠ 0 .

Definition: Limits

A limit can be defined as the value that a function or sequence approaches as the input or index approaches a certain point. It represents the behavior or trend of the function or sequence near that particular point.

Explanation:

Here, the given image shows the limit of a function of x equals A as and when x approaches a.

Definition: Continuity

Continuity, in the context of mathematics and functions, refers to the smooth and unbroken nature of a function’s graph or behavior. It implies that there are no abrupt jumps, breaks, or holes in the graph of the function within a certain interval or over its entire domain.

More formally, a function f(x) is considered continuous at a point x = a if three conditions are satisfied.

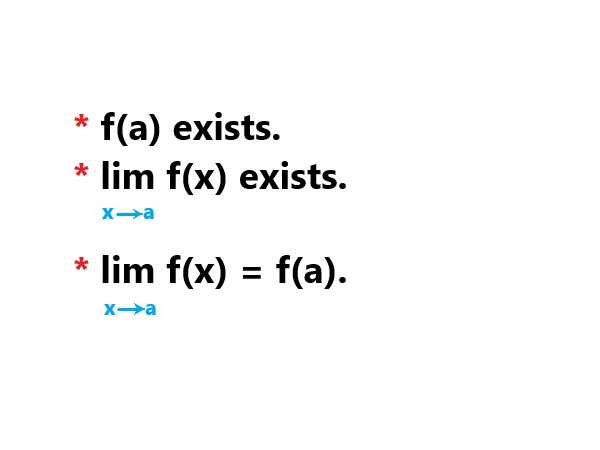
Explanation:

Here, the given image shows the three conditions that are

The function is defined at x = a.

The limit of the function as x approaches a exists.

The limit of the function as x approaches a is equal to the value of the function at x = a.

If these conditions hold for every point in the domain of the function, then the function is said to be continuous over its entire domain.