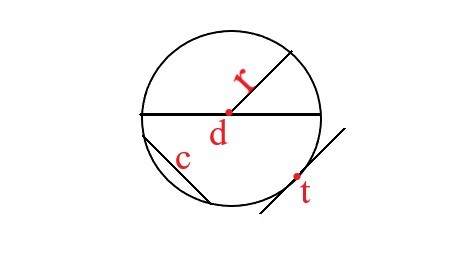
Definition: Circle

A circle is a geometric shape consisting of all points in a plane that are at a constant distance, known as the radius, from a fixed point, called the center.

The total distance around the circle, calculated as C = 2πr.

The total region enclosed by the circle, given by \$A = πr^2\$.

Explanation:

In this image, the parts of a circle are radius(r), diameter(d), chord(c), tangent(t).

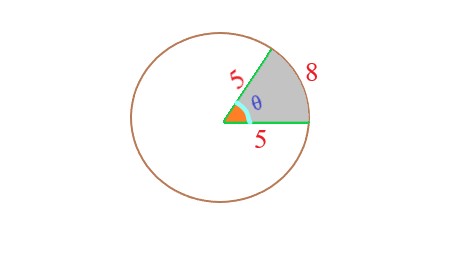
Definition: Area of Sector

A sector of a circle is a portion of the circle enclosed by two radii and an arc between them. The area of a sector can be calculated using the formula: Area of Sector = \$("Central Angle"/(360°)) × πr^2\$, where Central Angle is the angle formed by the radii at the center of the circle (measured in degrees), and r is the radius of the circle.

Explanation:

In this image, the radius of 5 units and an arc length of 8 units, the sector of the circle defined by this arc length has an area of 20 square units, as determined by the formula: \$A = (s \times r)/2\$

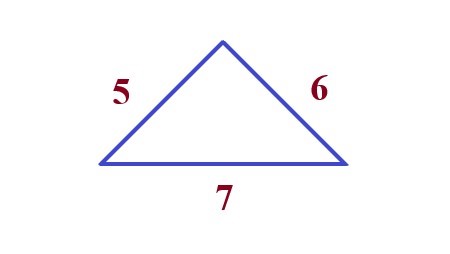
Definition: Triangle

A triangle is a polygon with three edges and three vertices. The three vertices are connected by line segments called sides, and the angles between these sides are called the interior angles. The sum of the interior angles of a triangle is always 180 degrees.

The area of a triangle can be calculated using various formulas, depending on the given information. The most common formula is: \$A = 1/2 \times b \times h\$, where b is base and h is height.

The perimeter of a triangle is the total length of its three sides. For a triangle with side lengths a, b, and c, the perimeter P is:

P = a + b + c

Explanation:

In this example, we need to find out the area of the triangle using the given three sides 5, 6, and 7 units in length \$\sqrt(s(s−a)(s−b)(s−c)}\$ then we get \$6\sqrt(6)\$ units.

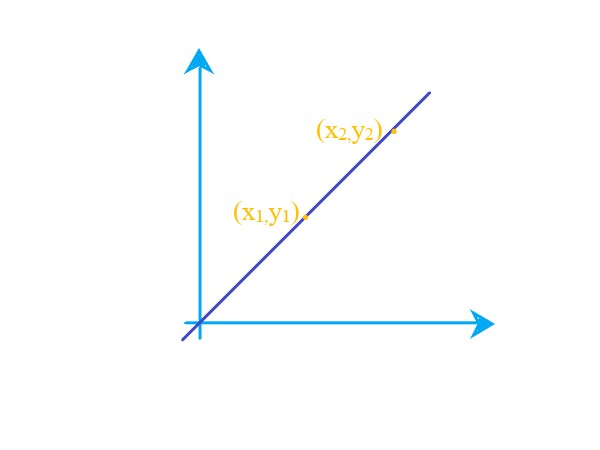
Definition: Slope of a Line

The slope of a line can be calculated using two points lying on a straight line. Given the coordinates of the two points, we can apply the slope of the line formula. Let the coordinates of those two points be, \$P_1 = (x_1, y_1)\$ \$P_2 = (x_2, y_2)\$.

Explanation:

To find the slope of a line, use an equation, \$m = (y_2 − y_1)/(x_2 − x_1)\$ where m is the slope of the line.