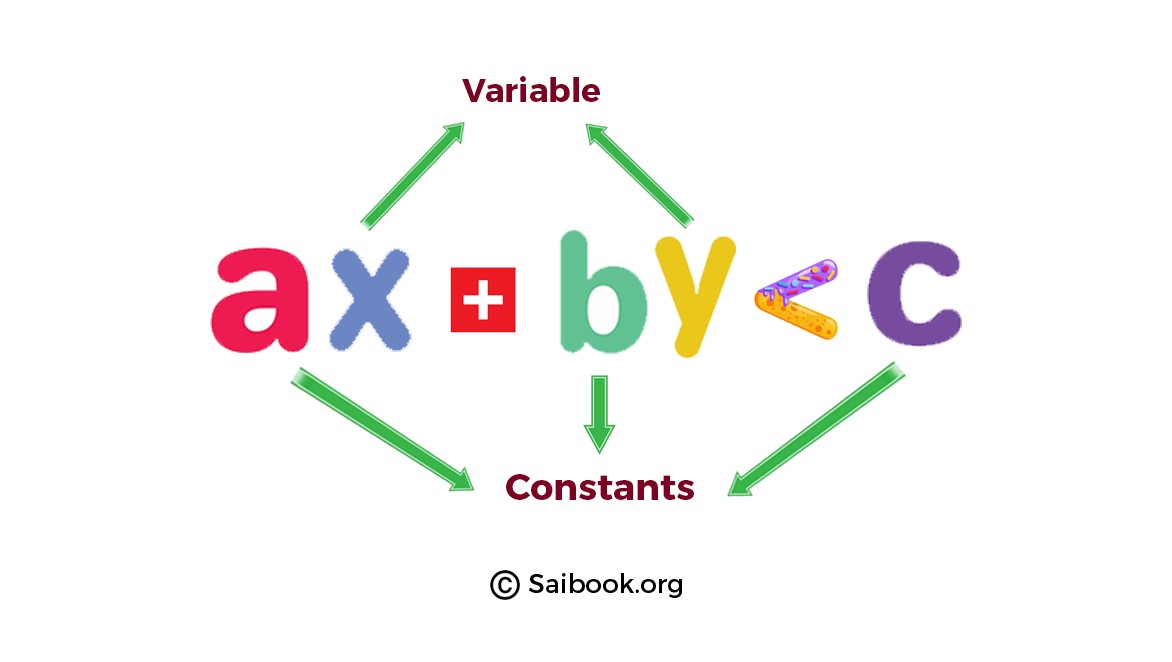Definition: Linear inequalities

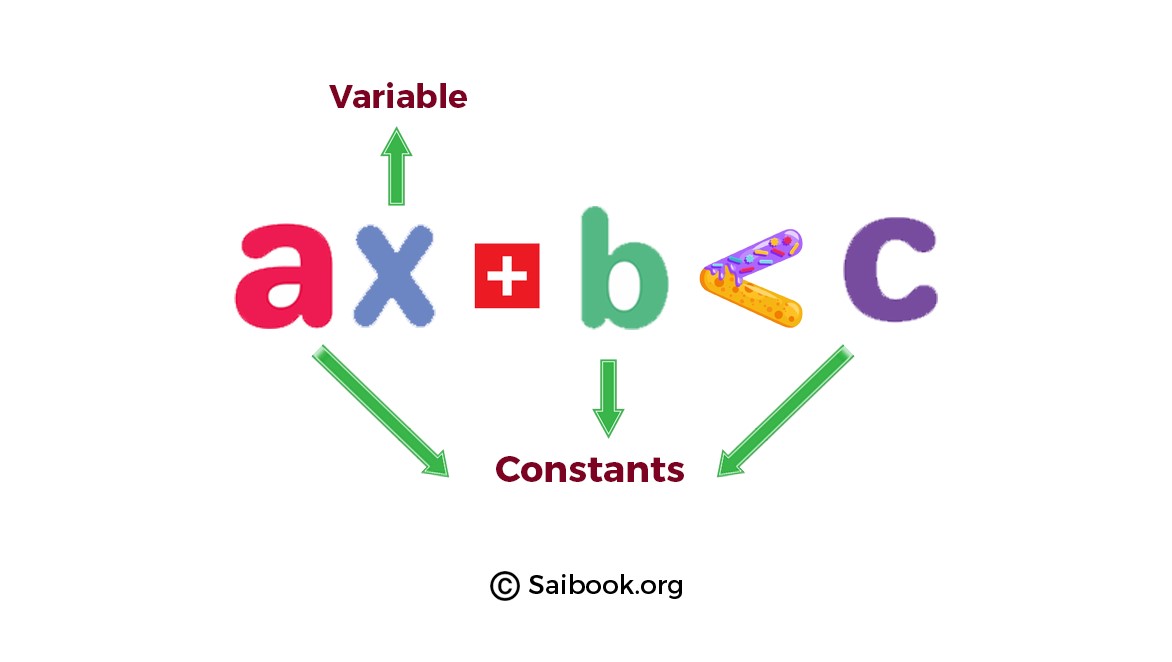
Linear inequalities are mathematical statements that express a relationship between two algebraic expressions using inequality symbols (<, >, ≤, or ≥). These inequalities involve linear equations, which consist of variables raised to the first power, multiplied or divided by constants.

The general form of a linear inequality is: ax + b < c.

Explanation:

The image illustrates the inequality ax + b < c, where x is the variable, and a, b, and c are constants.

Definition: Linear inequalities in one variable

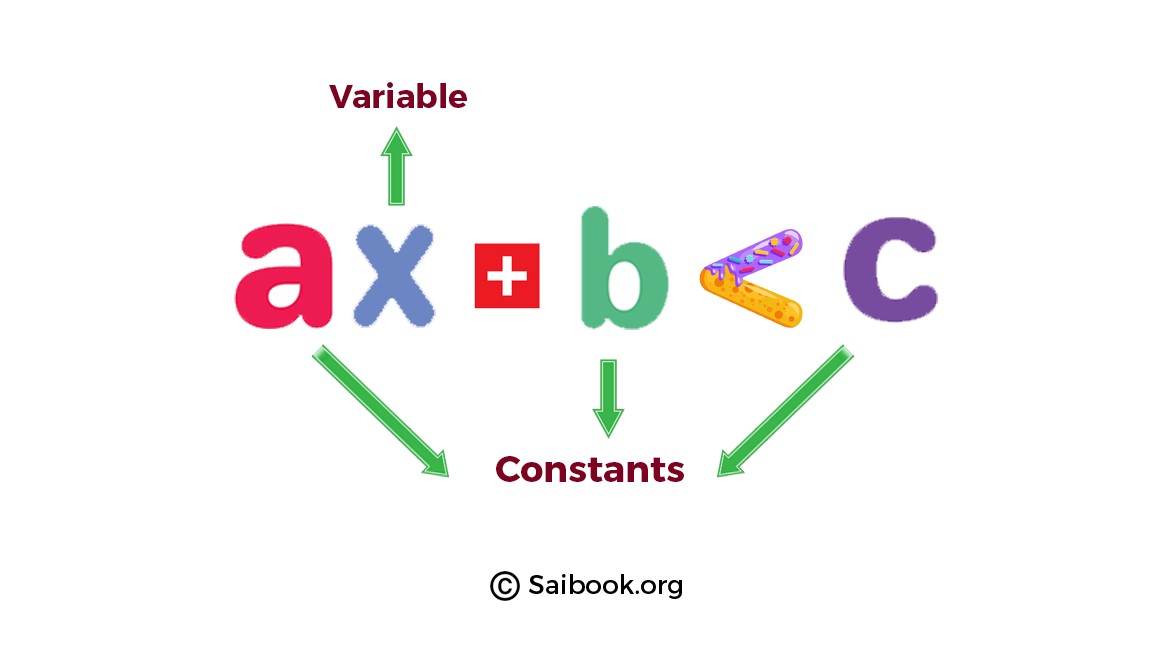
Linear inequalities in one variable are mathematical statements that involve a variable raised to the power of 1 and a linear function. These inequalities express a relationship between the variable and a constant value, indicating whether the variable is greater than, less than, or equal to that constant.

The general form of a linear inequality in one variable is: ax + b < c.

Explanation:

The given image illustrates the inequality ax + b < c, where x is the variable, and a, b, and c are constants.

Definition: Linear inequalities in two variable

Linear inequalities in two variables refer to mathematical statements that involve two variables and represent relationships between them using inequality symbols such as "<" (less than), ">" (greater than), "\$ le\$" (less than or equal to), or "\$ ge\$" (greater than or equal to).

The general form of a linear inequality in two variables is: ax + by < c.

Explanation:

Here the given image shows the ax + by < c, where x and y represent the variables, a, b, and c are constants.