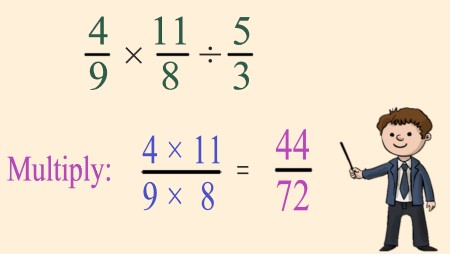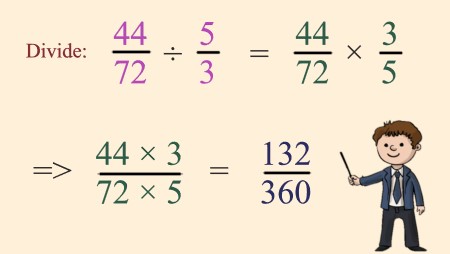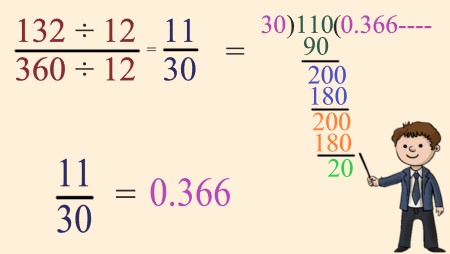SaiBook.us Math

Home Course Section Lesson

Lesson Topics Discussion Quiz: Class Homework

Example1

Title: Decimal Equivalent Fraction

Grade Lesson s2-l4

Explanation: The best way to understand SAT-4 is by looking at some examples. Take turns and read each example for easy understanding.

Examples

Topics → Definition Example1

Solve the expression \$4/9 × 11/8 ÷ 5/3\$.

Step: 1

First, multiply the fractions \$4/9\$ and \$11/8\$.
The result of this calculation is \$(4 times 11)/(9 times 8)\$ = \$44/72\$.

$1a$

. https://uat-image.saibook.org/edu/math/psat/v4/psat-core/s2/l4/example1/1a.jpg

Explanation:

In this step, begin by multiplying the fractions. The result is \$44/72\$.

Step: 2

Now, divide the resultant fraction by \$5/3\$ .
Division of fractions is the same as multiplying by the reciprocal. Rewrite the division (\$÷ 5/3\$) as multiplication by its reciprocal (\$× 3/5\$):
⇒ \$44/72 \times 3/5\$ = \$132/360\$

$2a$

. https://uat-image.saibook.org/edu/math/psat/v4/psat-core/s2/l4/example1/2a.jpg

Explanation:

In this step,Division of fractions is equivalent to multiplying by the reciprocal. Therefore, dividing by \$5/3\$ is rewritten as multiplying by its reciprocal, \$3/5\$, then we get \$132/360\$

Step: 3

Find the greatest common divisor (GCD) of 132 and 360. The GCD is 12. Divide both numerator and denominator by 12:
\$132/360 \div 12/12\$ = \$11/30\$.
Hence the decimal number after dividing the resultant fraction \$11/30\$ = 0.366.

$3a$

. https://uat-image.saibook.org/edu/math/psat/v4/psat-core/s2/l4/example1/3a.jpg

Explanation:

The greatest common divisor (GCD) of 132 and 360 is 12. By dividing the numerator and denominator by 12, we get \$11/30\$. Converting \$11/30\$ to a decimal gives 0.366.