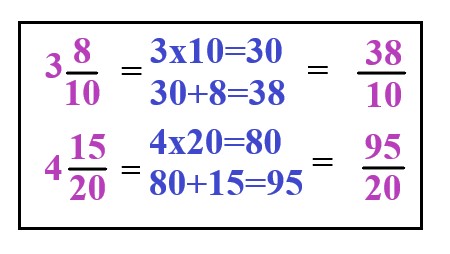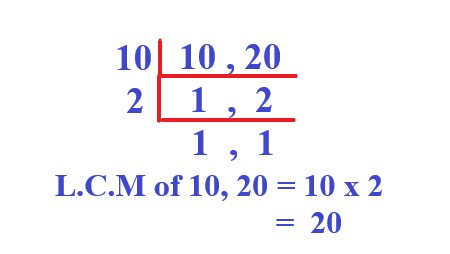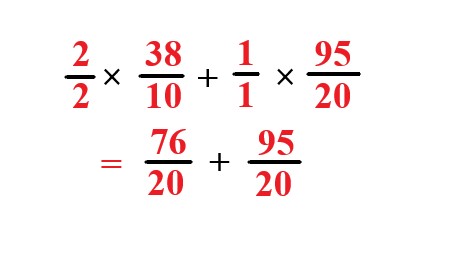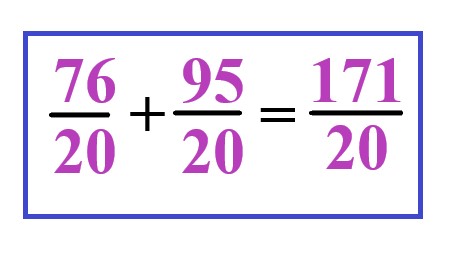SaiBook.us Math

Home Course Section Lesson

Lesson Topics Discussion Quiz: Class Homework

Example1

Title: Fraction Addition

Grade Lesson s1-l5

Explanation: The best way to understand SAT-4 is by looking at some examples. Take turns and read each example for easy understanding.

Examples

Topics → Definition Example1

Add \$3 8/10\$ + \$4 15/20\$.

Step: 1

First, convert the given mixed fractions into improper fractions.
\$3 8/10\$ = \$38/10\$
\$4 15/20\$ = \$95/20\$

$1a$

. https://uat-image.saibook.org/edu/math/psat/v4/psat-core/s1/l5/example1/1a.jpg

Explanation:

Convert the given mixed fractions to improper fractions.
Multiply 3 by 10 and then add 8. The result is 38.
Multiply 4 by 20 and then add 15. The result is 95.

Step: 2

The denominators are 10 and 20. The least common Multiply (LCM) between 10 and 20 is 20.

$2a$

. https://uat-image.saibook.org/edu/math/psat/v4/psat-core/s1/l5/example1/2a.jpg

Explanation:

In this step, the denominators are different, so we need to find the Least Common Multiple (LCM). The LCM of 10 and 20 is 20.

Step: 3

To make the denominators equal, we must multiply + \$2/2\$ \$\times\$ \$38/10\$ = \$76/20\$
\$1/1\$ \$\times\$ \$95/20\$ = \$95/20\$.

$3a$

. https://uat-image.saibook.org/edu/math/psat/v4/psat-core/s1/l5/example1/3a.jpg

Explanation:

We already have one fraction with a denominator of 20 (\$95/20\$), so we’ll convert \$38/10\$ to have 20 as the denominator.

To do this, multiply both the numerator and denominator of \$38/10\$ by 2:
\$2/2\$ \$\times\$ \$38/10\$ = \$76/20\$

Step: 4

Now that both fractions have the same denominator, add the numerators:
⇒ \$76/20\$ + \$95/20\$ = \$171/20\$

$4a$

. https://uat-image.saibook.org/edu/math/psat/v4/psat-core/s1/l5/example1/4a.jpg

Explanation:

In this step, find the sum of the fractions, add their numerators, and keep the denominator as 20. The result is \$171/20\$.