Lesson Topics Discussion Quiz: Class Homework |
Definition1 |
Title: Fractions |
Grade Lesson s1-p2 |
Explanation: The best way to understand PSAT-4 is by looking at some definitions. Take turns and read each definition for easy understanding. |
Definition
Topics → Definition Example1 Example2
Definition: Addition Fraction |
|
|
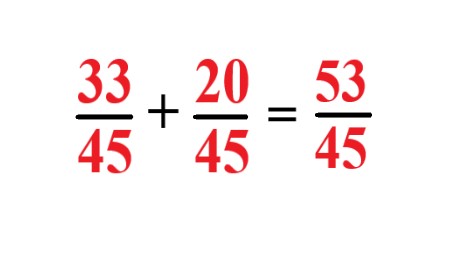
. |
Explanation: |
|
Here, the sum of \$33/45\$ and \$20/45\$ is \$53/45\$. |
|
Definition: Subtraction Fraction |
|
|
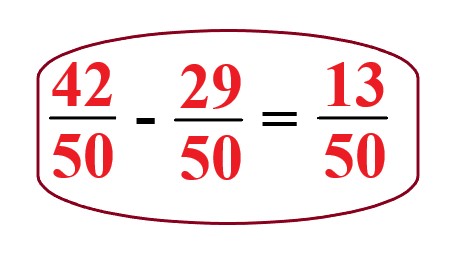
. |
Explanation: |
|
In this image, the difference between of \$42/50\$ and \$29/50\$ is \$13/50\$. |
|
Definition: Multiplication Fraction |
|
|

. |
Explanation: |
|
Multiply the fractions \$3 14/5 \times 4/5\$ then we get \$4 16/25\$. |
|
Definition: Division Fraction |
|
|
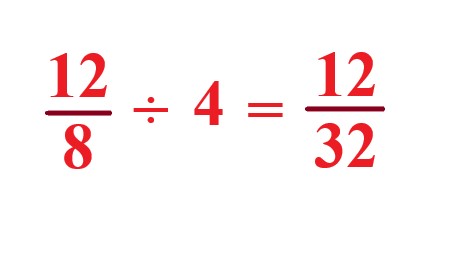
. |
Explanation: |
|
Divide the fraction \$12/8 \div 4\$, reciprocal the second fraction \$12/8 \times 1/4\$ then we get \$12/32\$. |
|
Copyright © 2020-2024 saibook.us Contact: info@saibook.org Version: 4.0 Built: 08-Oct-2025 12:00PM EST