SaiBook.us Math

Home Course Section Lesson

Lesson Topics Discussion Quiz: Class Homework

Example1

Title: Area of Square

Grade 6+ Lesson s1-l5

Explanation: The best way to understand geometry is by looking at some examples. Take turns and read each example for easy understanding.

Examples

Topics → Definition Example1 Example2

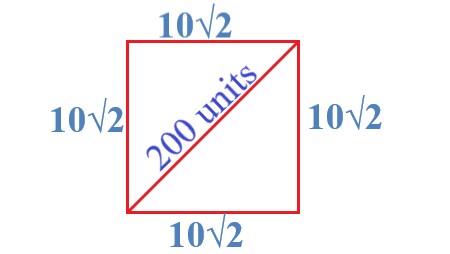
The diagonal of a square is 20 units. Find the area & length of each side of the square.

$40%$

Step: 1

In this case, let’s assume that each side of the square has a length of x units. A square’s diagonal is 20 units.
Applying the Pythagorean theorem,\$x^2 + x^2 = 20^2\$
⇒ \$2x^2\$ = 400.
Dividing both sides by 2:\$ x^2 = 200\$

Explanation:

In this step, let’s assume that each side of the square has a length of x units. The given diagonal of the square is 20 units. When we apply the Pythagorean theorem to the equation, we get \$x^2 + x^2 = 20^2\$. Simplifying it, we get 2x^2 = 400, and then further simplifying to \$x^2 = 200\$.

Step: 2

Taking the square root of both sides, to find:
x = √200
Simplifying further, to get:
x = √(100 × 2) = 10√2
Therefore, each side of a square is 10√2 units.

Explanation:

By taking the square root of 200, we get x = 10√2.Therefore, the length of each side of the square is 10√2 units.

Step: 3

To find the area of a square:
\$Area = side \times side = 10√2 \times 10√2 = 200 sq.units\$
Hence, the area of a square is 200 sq. units.

Explanation:

In this step, find the area of a square. The formula is \$side \times side\$, which means, in this case, it’s \$10√2 \times 10√2\$. Therefore, the area is 200 sq. units.