SaiBook.us Geometry

Lesson Example Discussion Quiz: Class Homework

Example

Title: Perpendiculer Lines

Grade: 6-a Lesson: S2-L8

Explanation: The best way to understand geometry is by looking at some examples. Take turns and read each example for easy understanding.

Examples:

Lines E and F, intersecting at points P(0, 6) and Q(4, 0), are specific lines. Determine the length of the intersecting line segment.

Step 1a

The distance formula for the line segment between points P(0, 6) and Q(4, 0) on lines E and F. The distance formula between two points \$"Distance" = \sqrt(("x"_2 - "x"_1)^2 + ("y"_2 - "y"_1)^2)\$

$1a$

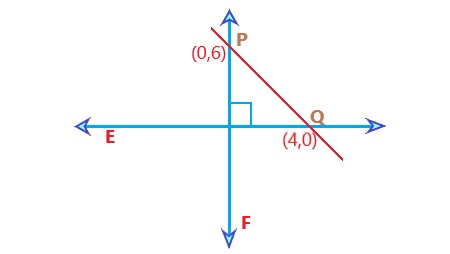
Explanation: The formula to calculate the distance between points P(0, 6) and Q(4, 0) on lines E and F is given by the distance formula: Distance : \$ \sqrt(("x"_2 - "x"_1)^2 + ("y"_2 - "y"_1)^2)\$

Step 1b

Substitute these coordinates into the formula: \$"Distance" = \sqrt((4 - 0)^2 + (0 - 6)^2)\$
\$"Distance" = \sqrt((4)^2 + (-6)^2)\$

Explanation: Insert these values into the equation: \$"Distance" = \sqrt((4 - 0)^2 + (0 - 6)^2)\$
This simplifies to: \$"Distance" = \sqrt((4)^2 + (-6)^2)\$

Step 1c

After simplifier the above equation: Distance = \$\sqrt(16 + 36 )\$
Distance = \$\sqrt(52)\$

Explanation: In this step, we are simplifying the above equation: Distance = \$\sqrt(52)\$

Step 1d

So, the length of the line segment between points P and Q on lines E and F is \$\sqrt(52)\$

Explanation: The line segment connecting points P and Q on lines E and F has a length represented by the square root of 52, denoted as \$\sqrt 52\$.