SaiBook.us Geometry

Lesson Example Discussion Quiz: Class Homework

Example

Title: Parallel Lines

Grade: 6-a Lesson: S2-L7

Explanation: The best way to understand geometry is by looking at some examples. Take turns and read each example for easy understanding.

Examples:

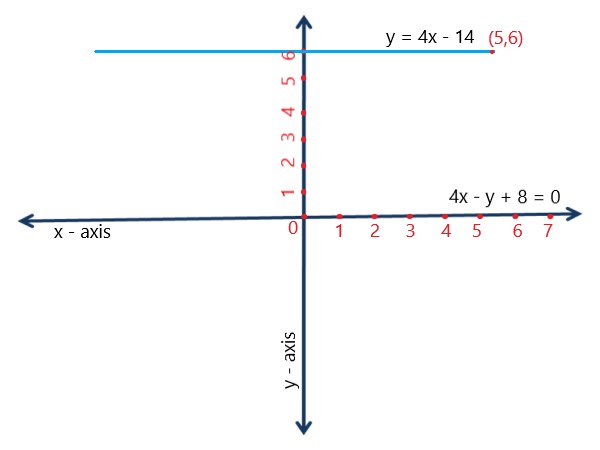
Find the equation of a straight line is passing through (5, 6) and parallel to the line 4x - y + 8 = 0.

Step 1a

The slope of a line is 4x - y + 8 = 0.
To do this, rearrange the equation into slope-intercept form (y = mx + c), where "m" is the slope:
y = 4x + 8
The original line has a slope denoted by the symbol m = 4.

$1a$

Explanation: Rearrange 4x - y + 8 = 0 to y = 4x + 8 in slope-intercept form. The slope (m) is 4.

Step 1b

To find a line parallel to the original, it must have the same slope, represented by "m", which, in this case, is 4.

Explanation: Since you want to find a line parallel to the original line, it will have the same slope, which is m = 4.

Step 1c

Using the slope (m = 4) and the point (5, 6), apply the point-slope form to discover the equation of the new line.
The point-slope form of a line’s equation is: y - y1 = m(x - x1).
Here(x1, y1) is a point on the line, and m is the slope.

Explanation: Now that you have the slope (m = 4) and a point (5, 6), you can use the point-slope form of the line equation to find the equation of the new line: y - y1 = m(x - x1).

Step 1d

Substituting the values: y - 6 = 4 (x - 5)
Rewrite and simplify the equation: y - 6 = 4x - 20

Explanation: Now plug the values into the equation(x1, y1) = (5, 6) and m = 4.
y - 6 = 4(x - 5).

Step 1e

Move numbers without variables to the right side: y = 4x - 20 + 6
After combining like terms, the simplified form is y = 4x - 14.

Explanation: In this step, Enhance and simplify the equation:
Start with y - 6 = 4x - 20.
Shift the constant terms to the right side: y = 4x - 20 + 6.
After combining like terms, it becomes y = 4x - 14.

Step 1f

So, the equation of the line passing through the point(5, 6) and parallel to the line 4x - y + 8 = 0 is y = 4x - 14.

Explanation: The line that goes through the point (5, 6) and is parallel to the line 4x - y + 8 = 0 can be expressed as
y = 4x - 14.