Step 1a

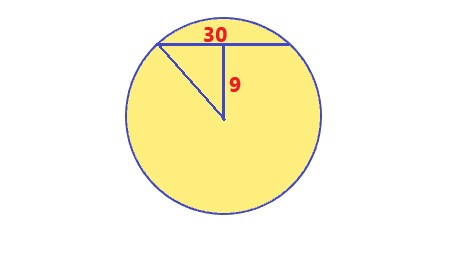
Explanation: With a chord length of 30 cm and a distance of 9 cm from the chord to the center, you can find the circle’s radius.

Step 1b

Now, we can use the Pythagorean Theorem to find the radius (r): \$r^2 = (c/2)^2 + h^2\$

Substitute the values: \$r^2 = (30/2)^2 + 9^2\$

⇒ \$r^2 = 15^2 + 9^2\$

⇒ \$r^2 = 225 + 81 = 306\$

Explanation: Using the Pythagorean Theorem, we can find the radius of a circle: \$ r^2 = (c/2)^2 + h^2\$. Substituting the values, we get \$r^2 = 306\$, so the radius is the square root of 306.

Step 1c

Apply square root r = \$\sqrt 306 sq.cm\$

After simplification r is 17.49 cm.

Explanation: In this step, Calculate the square root of 306 square centimeters. After simplification, the result is 17.49 cm.

Step 1d

Now we know the radius, can calculate the area (A) of the circle using the formula for the area of a circle: \$A = π \times r^2\$

Explanation: In this step, we can calculate the area of a circle by multiplying the radius squared by pi (π).

Step 1e

Now plug the values into the formula: \$A = 3.14 \times (17.49)^2\$

A = 960.52 sq.cm

Explanation: Compute A by using \$A = 3.14 x (17.49)^2\$. A = 960.52 sq .cm.

Step 1f

So, the area of the circle is approximately 960.52 sq.cm.

Explanation: The area of the circle is around 960.52 square centimeters.