SaiBook.us Geometry

Lesson Example Discussion Quiz: Class Homework

Example

Title: Geometry

Grade: 4-a Lesson: S3-L8

Explanation: The best way to understand geometry is by looking at some examples. Take turns and read each example for easy understanding.

Examples:

The volume of a cone with a height of 10 meters is 262 cubic meters. Find its total surface area.

Step 1a

Given the height of a cylinder is 10 meters and its volume is 262 cubic meters, find the radius. The formula gives the volume of a cone: \$V = 1/3 πr^2h\$

$1a$

Explanation: In this step, we can easily determine the radius of a cylinder with a height of 10m and a volume of 265 cubic meters using the formula for cylinder volume. \$V = 1/3 πr^2h\$

Step 1b

Plug the values into the formula: 262 = \$1/3 times 3.14 r^2 times 10\$

Simplify the above equation: \$262 = 10.47 times r^2 \$

Solve for r and apply square root on both sides of the equation: r = \$\sqrt (265/10.47)\$

r = \$\sqrt 25.02\$

r = 5

Explanation: To solve the problem, plug values into the formula: \$262 = 1/3 times 3.14 times r^2 times 10\$. Simplify to \$262 = 10.47 times r^2\$. Solve for r using square root, giving r = 5.

Step 1c

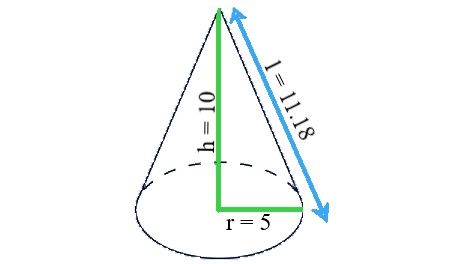
To find the slant height of a right circular cone, we can use the Pythagorean theorem.

The slant height (l) can be calculated using the formula: \$"l" = \sqrt(r^2 + h^2)\$

Substitute these values into the formula: \$"l" = \sqrt(5^2 + 10^2)\$

\$"l" = \sqrt(25 + 100)\$

\$"l" = \sqrt 125\$

l = 11.18

Therefore, the slant height of the cone is 11.18 units.

Explanation: In this step, to find the slant height of a right circular cone, use the Pythagorean theorem:

\$"l" = \sqrt(r^2 + h^2)\$. For example, if r is 5 and h is 10 units, the slant height is 11.18 units.

Step 1d

To find the lateral surface area(Al) using the formula: Al = πrl

Al = \$3.14 times 5 times 11.18\$

Al = 175.526

Explanation: In this step, to find the lateral surface area (Al), use the formula Al = πrl. For this specific shape, \$"Al" = 3.14 times 5 times 11.18 = 175.526\$.

Step 1e

The base area (Ab) is given by: Ab = \$πr^2\$

Ab = \$3.14 times 5^2\$

Ab = 78.5

Explanation: In this step, to find the base area (Ab), use the formula \$"Ab" = πr^2\$, where r is the radius. For this object, Ab = 78.5.

Step 1f

The total surface area(T) is the sum of the lateral surface area and the base area: T = Al + Ab

T = 175.526 + 78.5

T = 254.026

Therefore, the total surface area of the cone is 254.026 sq.mtrs.

Explanation: Finally, to calculate the total surface area of a cone (T), we add the lateral surface area (Al) and base area (Ab): T = Al + Ab. Hence, the total surface area of the cone is 254.026 sq.mtrs.