Lesson Example Discussion Quiz: Class Homework |
Example |
Title: Volume of Pyramid |
Grade: 4-a Lesson: S3-L7 |
Explanation: The best way to understand geometry is by looking at some examples. Take turns and read each example for easy understanding. |
Examples:
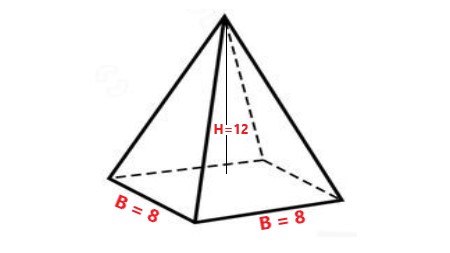
A square pyramid with a base side length of 8 units and a height of 12 units. Calculate the volume of the pyramid.
Step 1a
|
|
The base of the shape has a side length of 8 units and the height of the shape is 12 units. |
. |
Explanation: In this step, we will explain the dimensions of the shape. The base side length is 8 units, and the height is 12 units. |
|
Step 1b
|
|
To calculate the volume of a square pyramid, you can use the following formula: \$"V" = 1/3 times "B" times "H"\$. To determine if the base of the pyramid is a square Base(B) = \$"side Length" times "side Length"\$. B = \$8 times 8\$ = 64 sq.units |
|
Explanation: In this step, to calculate the volume of a square pyramid, use the formula \$"V" = 1/3 times "B" times "H"\$. To find the base (B), use the formula \$"B" = "side length" times "side length"\$. Plug the values into the base formula. The side length is 8 units, then B = 64 sq.units. |
|
Step 1c
|
|
Plug the values into the volume of the pyramid: \$"V" = 1/3 times 64 times 12\$ \$"V" = 1/\cancel3^1 times 64 times \cancel12^4\$ \$"V" = 256 "cubic units"\$ The volume of the square pyramid is 256 cubic units. |
|
Explanation: In this step, we substitute the known values into the pyramid volume formula, \$"V" = 1/3 times "base area" times "height"\$. The final calculation, \$"V" = 1/3 times 64 times 12\$, yields the volume of the pyramid as 256 cubic units. |
|
Copyright © 2020-2024 saibook.us Contact: info@saibook.us Version: 1.5 Built: 09-January-2023 08:10 PM EST