SaiBook.us Geometry

Lesson Example Discussion Quiz: Class Homework

Example

Title: Volume of 3d-shapes(cone , cylinder)

Grade: 4-a Lesson: S3-L4

Explanation: The best way to understand geometry is by looking at some examples. Take turns and read each example for easy understanding.

Examples:

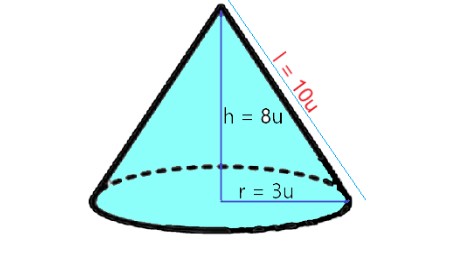
What is the height of a cone with a slant height of 10 units and a radius of 6 units, to calculate the volume of the cone?

Step 1a

Given that the slant height (l) is 10 units and the radius (r) is 6 units.

To find the height(h) by using the formula:

h = \$\sqrt(l^2 - r^2\$

Plug the values into the formula:

h = \$\sqrt(10^2 - 6^2)\$

h = \$\sqrt(100 - 36)\$

h = \$\sqrt 64\$

h = 8

So, the height is 8 units.

$1a$

Explanation: In this step, to find the height (h), use the formula: h = \$\sqrt(l^2 - r^2)\$. For l = 10 and r = 6, h = 8 units.

Step 1b

Find the volume of the cone: V = \$1/3 πr^2h\$

Plug the values into the formula: V = \$1/3(3.14)(6)^2(8)\$

V = \$904.32/3\$

V = 301.44 cubic units.

So, the volume of the cone is 301.33 cubic units.

Explanation: In this step, we can calculate the volume of a cone using the formula V = \$1/3πr²h\$. We can plug the given values of r and h into the formula, \$V = 1/3(3.14)(6)^2(8)\$. Therefore, the volume of the cone is 301.33 cubic units.

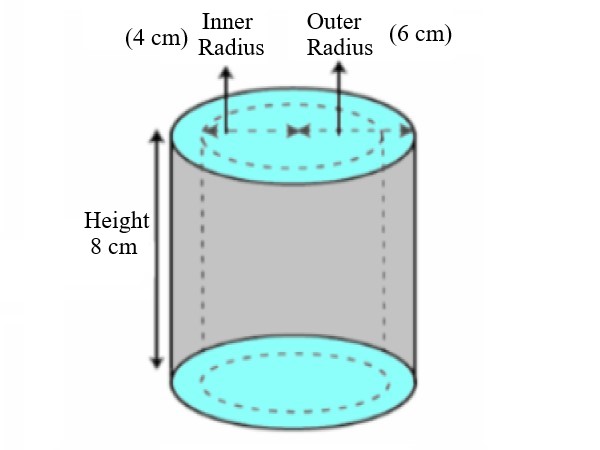
A pipe with an outer radius of 6 centimeters, an inner radius of 4 centimeters, and a height of 8 centimeters. Find the volume of the hallow cylinder.

Step 2a

Given the values of Outer radius \$(R)\$ as 6 cm, Inner radius (r) as 4 cm, and Height (h) as 8 cm.

$2a$

Explanation: In this step, explain the provided values of outer radius \$(R)\$ as 6 cm, inner radius(r) as 4 cm, and height (h) as 8 cm.

Step 2b

The formula for the volume of a hallow cylinder is: \$V = πh(R^2 - r^2)\$

Plug the values into the formula: \$V = 3.14(8)(6^2 - 4^2)\$

Explanation: In this step, Use the hallow cylinder volume formula \$V = πh(R^2 - r^2)\$, then substitute values

\$V = 3.14(8)(6^2 - 4^2)\$ to calculate.

Step 2c

Calculate the volume: V = 3.14(8)(36 - 16)

V = 502.4

So, the approximate volume of the hallow cylinder is 502.4 \$"cm"^3\$.

Explanation: Calculate the volume: V = 3.14(8)(36 - 16). V = 502.4. Therefore, the approximate volume of the hallow cylinder is 502.4 cm³.